Browse Source
Updated my cs review blog post with information on DFA minification, the pumping lemma and Context free languages.
pull/29/head
8 changed files with 261 additions and 97 deletions
Split View
Diff Options
-
+0 -97blogContent/posts/programming/CS -Theory-Exam-2-Review.md
-
+256 -0blogContent/posts/programming/cs-theory-exam-2-review.md
-
BINblogContent/posts/programming/media/CSTHEORY/DFAMinification.png
-
+1 -0blogContent/posts/programming/media/CSTHEORY/MinTable2.svg
-
+1 -0blogContent/posts/programming/media/CSTHEORY/MinificationTable.svg
-
+1 -0blogContent/posts/programming/media/CSTHEORY/MinimalDFA.svg
-
+1 -0blogContent/posts/programming/media/CSTHEORY/PumpingLemmaExample.svg
-
+1 -0blogContent/posts/programming/media/CSTHEORY/PumpingLemmaTheory.svg
+ 0
- 97
blogContent/posts/programming/CS -Theory-Exam-2-Review.md
View File
| @ -1,97 +0,0 @@ | |||
| This a very high level review post that I am making for myself and other people taking CS Theory. | |||
| If you want to lean about the theory behind the content in this blog post I recommed looking else where. | |||
| This post will cover how to solve typical problems relating to topics covered by my second CS Theory exam. | |||
| ## Myhill-Nerode Theorem | |||
| ### Definition | |||
| L is regular if and only if it has a finite index. The index is the maximum number of elements thar are pairwise distibguishable. | |||
| Two strings are said to be pairwise distinguishable if you can append something to both of the strings and it makes one string | |||
| accepted by the language and the other string non-accepting. | |||
| The size of an index set X equals the number of equivalence classes it has. Each element in the language is accepted by only | |||
| one equivalence class. | |||
| ### Problem Approach | |||
| Prove that language L is regular. | |||
| 1) Define a set X which is infinite in size - this doesn;t necesarrily need to be in the language. | |||
| 2) Make a general argument that show that each element in X is pairwise distinguishable. | |||
| Pick any two elements x, y in X and show that if you append z to them one is accepted by the language and | |||
| the other is not in the language. | |||
| ### Example | |||
| Prove the following language is non-regular: | |||
| $$ | |||
| L={ww^r | w \in {0,1}^*} | |||
| $$ | |||
| answer: | |||
| 1) | |||
| $$ | |||
| X = {(01)^i | i \geq 0} | |||
| $$ | |||
| Pick any 2 elements of X and show pairwise distinguishable | |||
| $$ | |||
| x = (01)^i, y = (01)^j | i \neq j | |||
| $$ | |||
| suppose we pick | |||
| $$ | |||
| z = (10)^i\\ | |||
| xz \in L\\ | |||
| yz \notin L | |||
| $$ | |||
| ## DFA minimization algorithm | |||
| Types of Problems: | |||
| - Prove DFA is minimal | |||
| - Minimize the DFA | |||
| The argument for DFA minimization comes from the Myhill-Nerode theorem. Given | |||
| a DFA, if you can form a set of strings which represent each state and they are all | |||
| pairwise distinguishable, then the DFA is minimal with that many states. | |||
| ### Prove DFA is minimal | |||
| For these types of problems you simply construct a table and show that each state is pairwise distinguishable. | |||
| To show pairwise distinguishability you have to show that there exists a string where if appened to one element | |||
| makes it accepted by the language but pushes the other string out of the language. | |||
| ex: Prove the following DFA is minimal. | |||
|  | |||
| $$ | |||
| X = {\epsilon, b, bb, ba} | |||
| $$ | |||
|  | |||
| ### Minimize the DFA | |||
| ## Pumping lemma for regular languages | |||
| ## Context-free grammars, closure properties for CFLs | |||
| ## Parse trees, ambiguity | |||
| ## Chomsky Normal Form | |||
| ## Pushdown automata | |||
| ## Construction to convert CFG to a PDA | |||
+ 256
- 0
blogContent/posts/programming/cs-theory-exam-2-review.md
View File
| @ -0,0 +1,256 @@ | |||
| This a very high level review post that I am making for myself and other people taking CS Theory. | |||
| If you want to lean about the theory behind the content in this blog post I recommed looking else where. | |||
| This post will cover how to solve typical problems relating to topics covered by my second CS Theory exam. | |||
| # Myhill-Nerode Theorem | |||
| ## Definition | |||
| L is regular if and only if it has a finite index. The index is the maximum number of elements thar are pairwise distibguishable. | |||
| Two strings are said to be pairwise distinguishable if you can append something to both of the strings and it makes one string | |||
| accepted by the language and the other string non-accepting. | |||
| The size of an index set X equals the number of equivalence classes it has. Each element in the language is accepted by only | |||
| one equivalence class. | |||
| ## Problem Approach | |||
| Prove that language L is regular. | |||
| 1) Define a set X which is infinite in size - this doesn;t necesarrily need to be in the language. | |||
| 2) Make a general argument that show that each element in X is pairwise distinguishable. | |||
| Pick any two elements x, y in X and show that if you append z to them one is accepted by the language and | |||
| the other is not in the language. | |||
| ## Example | |||
| Prove the following language is non-regular: | |||
| $$ | |||
| L={ww^r | w \in {0,1}^*} | |||
| $$ | |||
| answer: | |||
| 1) | |||
| $$ | |||
| X = {(01)^i | i \geq 0} | |||
| $$ | |||
| Pick any 2 elements of X and show pairwise distinguishable | |||
| $$ | |||
| x = (01)^i, y = (01)^j | i \neq j | |||
| $$ | |||
| suppose we pick | |||
| $$ | |||
| z = (10)^i\\ | |||
| xz \in L\\ | |||
| yz \notin L | |||
| $$ | |||
| # DFA minimization algorithm | |||
| Types of Problems: | |||
| - Prove DFA is minimal | |||
| - Minimize the DFA | |||
| The argument for DFA minimization comes from the Myhill-Nerode theorem. Given | |||
| a DFA, if you can form a set of strings which represent each state and they are all | |||
| pairwise distinguishable, then the DFA is minimal with that many states. | |||
| ## Prove DFA is minimal | |||
| For these types of problems you simply construct a table and show that each state is pairwise distinguishable. | |||
| To show pairwise distinguishably you have to show that there exists a string where if appended to one element | |||
| makes it accepted by the language but pushes the other string out of the language. | |||
| ### Example | |||
| Prove the following DFA is minimal. | |||
|  | |||
| Find a set of strings which represent the minimal path to each state in the DFA. | |||
| $$ | |||
| X = \{\epsilon, b, bb, ba\} | |||
| $$ | |||
| Show that each state is pairwise distinguishable. | |||
|  | |||
| ## Minimize the DFA | |||
| To use this concept of being indistinguishable to minimize a DFA, you can use a table to keep track which | |||
| states are distinguishable from each other. The states which are not indistinguishable can | |||
| be combined. To solve one of these problems you start by creating a table which compares each of the | |||
| states in the DFA. You then go through and mark the states which are indistinguishable -- start with | |||
| the ones with different accepting statuses. Then you continue marking off states where if you transition with | |||
| a symbol on the DFA you are distinguishable and the other state is non-distinguishable according to the table. | |||
| ### Example | |||
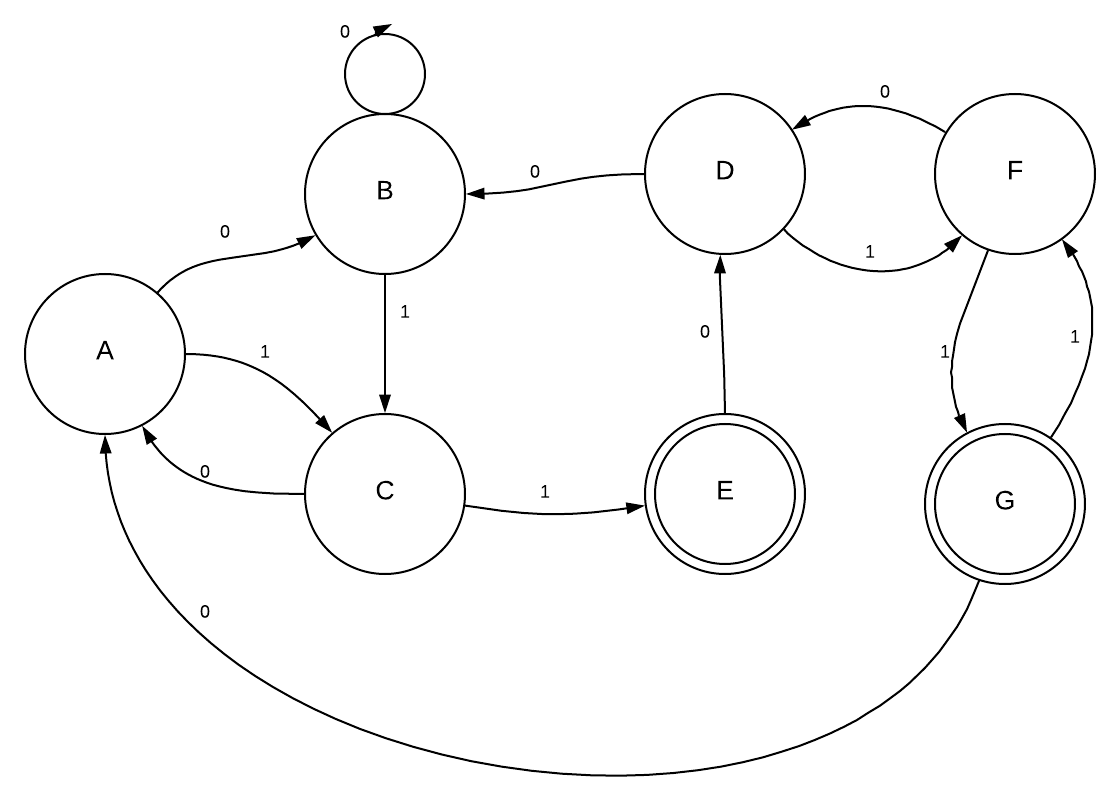
| Minify the Following DFA: | |||
|  | |||
| After marking the states with different accepting criteria as being distinguishable you get this table: | |||
|  | |||
| After looping through all pairs and marking them on the table if there exists symbol which results in one state | |||
| to be distinguishable and one to be indistinguishable you get this table: | |||
|  | |||
| According to the table you are able to combine {D, A, B}, {C, F}, and {E, G}. | |||
| Minimal DFA: | |||
|  | |||
| # Pumping lemma for regular languages | |||
| The pumping lemma cannot prove that a language is regular, however, you can use it | |||
| to show that some languages are non-regular. This theory gets at the idea that if | |||
| a regular language is long enough/infinite, it will have a state somewhere which is | |||
| repeated on the path that accepts the string. | |||
| The accepted strings can be divided into three parts: | |||
| - Symbols leading up to the loop | |||
| - Symbols which complete a loop and come back to start of loop | |||
| - Symbols at the end of the string | |||
|  | |||
| To Show that a language L is not regular using pumping lemma: | |||
| - Proof by Contradiction | |||
| - Assume L is regular | |||
| - Choose a representative string S which is just barely in the language and is represented in terms of p. | |||
| - Express S = xyz such that |xy| < p and y > 0 | |||
| - Show that you can pump y some amount of times such that it is not in the language. | |||
| - This contradicts the pumping lemma. | |||
| - The assumption that L is regular is wrong. | |||
| - L must not be regular. | |||
| ## Example | |||
| Show that the following language is non-regular. | |||
| $$ | |||
| {0^n1^n | n \geq 0} | |||
| $$ | |||
| Proof by contradiction | |||
| Assume that L is regular. | |||
| Let p be the pumping length associated with L | |||
| $$ | |||
| S = o^p1^p | |||
| $$ | |||
| S is valid since | |||
| $$ | |||
| |s| \geq p, S \in L | |||
| $$ | |||
| For any valid decomposition | |||
| S = xyz | |||
| such that |xy| <= p and |y| > 0 | |||
| Consider: | |||
| $$ | |||
| xy^2z | |||
| $$ | |||
| By the pumping lemma this should be in the language but it is not. Therefore our assumption that the | |||
| language is regular is false. | |||
|  | |||
| # Context-free grammars, closure properties for CFLs | |||
| The context-free grammars are a superset of the regular languages. This means that CFG's can represent | |||
| some non-regular languages and every regular language is also a CFL. Contest-free Languages are defined by Context-Free Grammars and accepted using | |||
| Pushdown Automata machines. | |||
| Context Free Grammars are Represented using: | |||
| - **Terminals** = Set of symbols in that language | |||
| - **Variables** = Set of symbols representing categories | |||
| - **Start Symbol** = Variable which you start with- written on top | |||
| - **Substitution Rules** = Set of rules that recursively define the language. | |||
| ## Example 1 | |||
| Grammar G: | |||
| $$ | |||
| A \rightarrow 0A1 \\ | |||
| A \rightarrow B \\ | |||
| B \rightarrow \# \\ | |||
| $$ | |||
| This grammar describes the following language: | |||
| $$ | |||
| L = \{0^k\#1^k | k \geq 0\} | |||
| $$ | |||
| ## Example 2 | |||
| Give CFG for non-Palindromes | |||
| $$ | |||
| S \rightarrow aXb | bXa | aSa | bSb | ab | ba \\ | |||
| X \rightarrow aX | bX | a | b \\ | |||
| $$ | |||
| In this example, the S rule states in that recursive state until something that is not a palindrome is found. | |||
| Once you exit the S state, you can finish by appending anything to the middle of the string. | |||
| ## Example 3 | |||
| Give CFG for the following language: | |||
| $$ | |||
| \{a^ib^jc^kd^l | i+k = j + l\} | |||
| $$ | |||
| $$ | |||
| S \rightarrow aSd | XYZ \\ | |||
| X \rightarrow aXb | \epsilon\\ | |||
| Y \rightarrow bYc | \epsilon\\ | |||
| Z \rightarrow cZd | \epsilon | |||
| $$ | |||
| # Parse trees, ambiguity | |||
| # Chomsky Normal Form | |||
| # Pushdown automata | |||
| # Construction to convert CFG to a PDA | |||