Updated my cs review blog post with information on DFA minification, the pumping lemma and Context free languages.

blogContent/posts/programming/CS -Theory-Exam-2-Review.md

@@ -1,97 +0,0 @@
-This a very high level review post that I am making for myself and other people taking CS Theory.
-If you want to lean about the theory behind the content in this blog post I recommed looking else where.
-This post will cover how to solve typical problems relating to topics covered by my second CS Theory exam.
-
-## Myhill-Nerode Theorem
-
-### Definition
-L is regular if and only if it has a finite index. The index is the maximum number of elements thar are pairwise distibguishable.
-Two strings are said to be pairwise distinguishable if you can append something to both of the strings and it makes one string
-accepted by the language and the other string non-accepting. 
-The size of an index set X equals the number of equivalence classes it has. Each element in the language is accepted by only
-one equivalence class.
-
-### Problem Approach
-
-Prove that language L is regular.
-
-1) Define a set X which is infinite in size - this doesn;t necesarrily need to be in the language.
-
-2) Make a general argument that show that each element in X is pairwise distinguishable.
-Pick any two elements x, y in X and show that if you append z to them one is accepted by the language and 
-the other is not in the language.
-
-### Example
-
-Prove the following language is non-regular:
-
-$$
-L={ww^r | w \in {0,1}^*}
-$$
-
-answer:
-
-1)
-
-$$
-X = {(01)^i | i \geq 0}
-$$
-
-Pick any 2 elements of X and show pairwise distinguishable
-
-$$
-x = (01)^i, y = (01)^j  | i \neq j
-$$
-
-suppose we pick
-$$
-z = (10)^i\\
-xz \in L\\
-yz \notin L
-$$
-
-
-## DFA minimization algorithm
-
-Types of Problems:
-- Prove DFA is minimal
-- Minimize the DFA
-
-The argument for DFA minimization comes from the Myhill-Nerode theorem. Given
-a DFA, if you can form a set of strings which represent each state and they are all 
-pairwise distinguishable, then the DFA is minimal with that many states.
-
-
-### Prove DFA is minimal
-
-For these types of problems you simply construct a table and show that each state is pairwise distinguishable.
-To show pairwise distinguishability you have to show that there exists a string where if appened to one element 
-makes it accepted by the language but pushes the other string out of the language.
-
-ex: Prove the following DFA is minimal.
-
-![DFA Example](media/CSTHEORY/DFAMinimalProof.png)
-
-$$
-X = {\epsilon, b, bb, ba}
-$$
-
-![DFA Example](media/CSTHEORY/Table.png)
-
-
-### Minimize the DFA
-
-
-
-## Pumping lemma for regular languages
-
-## Context-free grammars, closure properties for CFLs
-
-## Parse trees, ambiguity
-
-## Chomsky Normal Form
-
-## Pushdown automata
-
-## Construction to convert CFG to a PDA
-

blogContent/posts/programming/cs-theory-exam-2-review.md

@@ -0,0 +1,256 @@
+This a very high level review post that I am making for myself and other people taking CS Theory.
+If you want to lean about the theory behind the content in this blog post I recommed looking else where.
+This post will cover how to solve typical problems relating to topics covered by my second CS Theory exam.
+
+# Myhill-Nerode Theorem
+
+## Definition
+L is regular if and only if it has a finite index. The index is the maximum number of elements thar are pairwise distibguishable.
+Two strings are said to be pairwise distinguishable if you can append something to both of the strings and it makes one string
+accepted by the language and the other string non-accepting. 
+The size of an index set X equals the number of equivalence classes it has. Each element in the language is accepted by only
+one equivalence class.
+
+## Problem Approach
+
+Prove that language L is regular.
+
+1) Define a set X which is infinite in size - this doesn;t necesarrily need to be in the language.
+
+2) Make a general argument that show that each element in X is pairwise distinguishable.
+Pick any two elements x, y in X and show that if you append z to them one is accepted by the language and 
+the other is not in the language.
+
+## Example
+
+Prove the following language is non-regular:
+
+$$
+L={ww^r | w \in {0,1}^*}
+$$
+
+answer:
+
+1)
+
+$$
+X = {(01)^i | i \geq 0}
+$$
+
+Pick any 2 elements of X and show pairwise distinguishable
+
+$$
+x = (01)^i, y = (01)^j  | i \neq j
+$$
+
+suppose we pick
+$$
+z = (10)^i\\
+xz \in L\\
+yz \notin L
+$$
+
+
+# DFA minimization algorithm
+
+Types of Problems:
+- Prove DFA is minimal
+- Minimize the DFA
+
+The argument for DFA minimization comes from the Myhill-Nerode theorem. Given
+a DFA, if you can form a set of strings which represent each state and they are all 
+pairwise distinguishable, then the DFA is minimal with that many states.
+
+
+## Prove DFA is minimal
+
+For these types of problems you simply construct a table and show that each state is pairwise distinguishable.
+To show pairwise distinguishably you have to show that there exists a string where if appended to one element 
+makes it accepted by the language but pushes the other string out of the language.
+
+### Example
+
+Prove the following DFA is minimal.
+
+![DFA Example](media/CSTHEORY/DFAMinimalProof.png)
+
+Find a set of strings which represent the minimal path to each state in the DFA.
+
+$$
+X = \{\epsilon, b, bb, ba\}
+$$
+
+Show that each state is pairwise distinguishable.
+
+![DFA Example](media/CSTHEORY/DFAMinimalTable.png)
+
+
+## Minimize the DFA
+
+To use this concept of being indistinguishable to minimize a DFA, you can use a table to keep track which
+states are distinguishable from each other. The states which are not indistinguishable can 
+be combined. To solve one of these problems you start by creating a table which compares each of the 
+states in the DFA. You then go through and mark the states which are indistinguishable -- start with 
+the ones with different accepting statuses. Then you continue marking off states where if you transition with
+a symbol on the DFA you are distinguishable and the other state is non-distinguishable according to the table.
+
+### Example
+
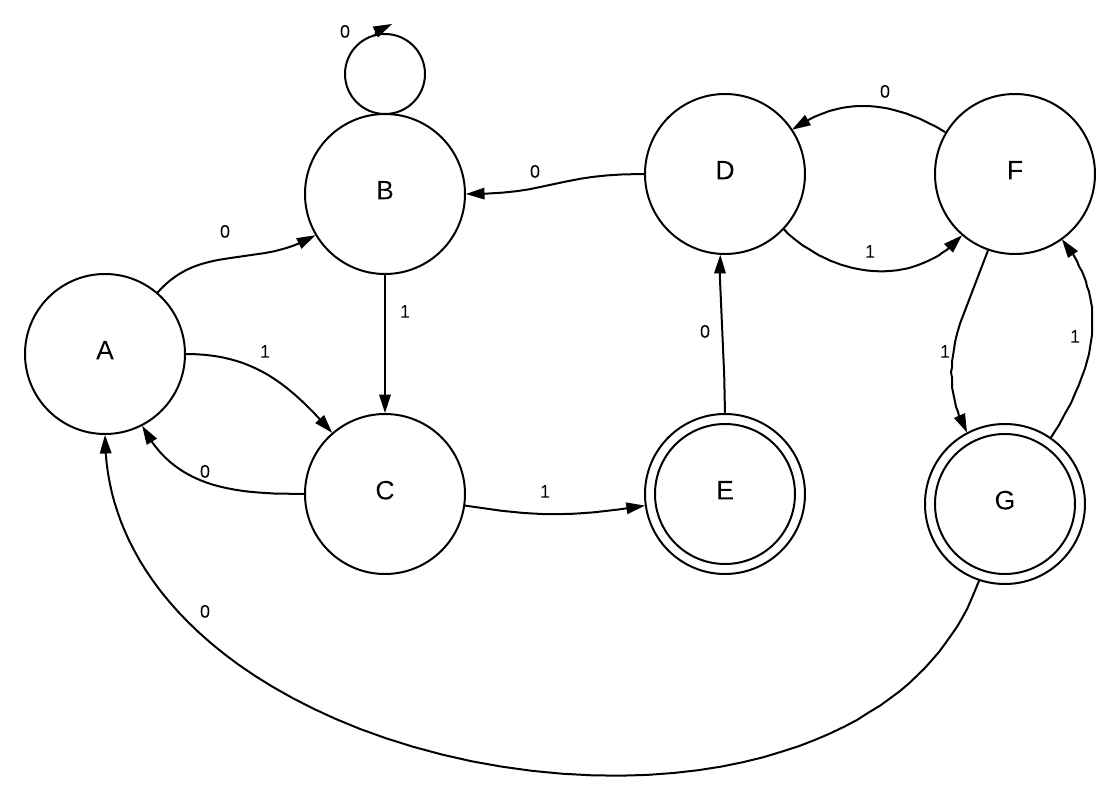
+Minify the Following DFA:
+
+![DFA Example](media/CSTHEORY/DFAMinification.png)
+
+After marking the states with different accepting criteria as being distinguishable you get this table:
+
+![Half Complete Table](media/CSTHEORY/MinificationTable.svg)
+
+
+After looping through all pairs and marking them on the table if there exists symbol which results in one state 
+to be distinguishable and one to be indistinguishable you get this table:
+
+![Min TableTable](media/CSTHEORY/MinTable2.svg)
+
+According to the table you are able to combine {D, A, B}, {C, F}, and {E, G}.
+
+Minimal DFA:
+
+![Min DFA](media/CSTHEORY/MinimalDFA.svg)
+
+
+# Pumping lemma for regular languages
+
+The pumping lemma cannot prove that a language is regular, however, you can use it
+to show that some languages are non-regular. This theory gets at the idea that if
+a regular language is long enough/infinite, it will have a state somewhere which is
+repeated on the path that accepts the string.
+
+The accepted strings can be divided into three parts:
+
+- Symbols leading up to the loop
+- Symbols which complete a loop and come back to start of loop
+- Symbols at the end of the string
+
+![Min DFA](media/CSTHEORY/PumpingLemmaTheory.svg)
+
+
+
+To Show that a language L is not regular using pumping lemma:
+
+- Proof by Contradiction
+- Assume L is regular
+- Choose a representative string S which is just barely in the language and is represented in terms of p. 
+- Express S = xyz such that |xy| < p and y > 0
+- Show that you can pump y some amount of times such that it is not in the language.
+- This contradicts the pumping lemma.
+- The assumption that L is regular is wrong.
+- L must not be regular.
+
+
+## Example
+
+Show that the following language is non-regular.
+
+$$
+{0^n1^n | n \geq 0}
+$$
+
+Proof by contradiction
+
+Assume that L is regular.
+
+Let p be the pumping length associated with L
+
+$$
+S = o^p1^p
+$$
+
+S is valid since
+
+$$
+|s| \geq p, S \in L
+$$
+
+For any valid decomposition
+
+S = xyz
+
+such that |xy| <= p and |y| > 0
+
+Consider:
+
+$$
+xy^2z
+$$
+
+By the pumping lemma this should be in the language but it is not. Therefore our assumption that the
+language is regular is false. 
+
+![Min DFA](media/CSTHEORY/PumpingLemmaExample.svg)
+
+# Context-free grammars, closure properties for CFLs
+
+The context-free grammars are a superset of the regular languages. This means that CFG's can represent 
+some non-regular languages and every regular language is also a CFL. Contest-free Languages are defined by Context-Free Grammars and accepted using
+Pushdown Automata machines.
+
+Context Free Grammars are Represented using:
+
+- **Terminals** = Set of symbols in that language
+- **Variables** = Set of symbols representing categories
+- **Start Symbol** = Variable which you start with- written on top
+- **Substitution Rules** = Set of rules that recursively define the language.
+
+## Example 1
+
+Grammar G:
+
+$$
+A \rightarrow 0A1 \\
+A \rightarrow B \\
+B \rightarrow \# \\
+$$
+
+
+This grammar describes the following language:
+
+$$
+L = \{0^k\#1^k | k \geq 0\}
+$$
+
+## Example 2
+
+Give CFG for non-Palindromes
+
+$$
+S \rightarrow aXb | bXa | aSa | bSb | ab | ba \\
+X \rightarrow aX | bX | a | b \\
+$$
+
+
+In this example, the S rule states in that recursive state until something that is not a palindrome is found.
+Once you exit the S state, you can finish by appending anything to the middle of the string. 
+
+
+## Example 3
+
+Give CFG for the following language:
+
+$$
+\{a^ib^jc^kd^l | i+k = j + l\}
+$$
+
+$$
+S \rightarrow aSd | XYZ \\
+X \rightarrow aXb | \epsilon\\
+Y \rightarrow bYc | \epsilon\\
+Z \rightarrow cZd | \epsilon
+$$
+
+# Parse trees, ambiguity
+
+# Chomsky Normal Form
+
+# Pushdown automata
+
+# Construction to convert CFG to a PDA
+