Add notes for decision based models (#1)

index.md

@@ -22,7 +22,7 @@ Starting with the Fall 2019 offering of CS 224W, the course covers three broad t
 3. [Influence Maximization](): Influential sets, submodularity, hill climbing
 4. [Outbreak Detection](): CELF, lazy hill climbing
 5. [Link Analysis](): PageRank and SimRank
-6. [Network Effects and Cascading Behavior](): Decision-based diffusion, probabilistic contagion, SEIZ
+6. [Network Effects and Cascading Behavior](network-methods/network-effects-and-cascading-behavior): Decision-based diffusion, probabilistic contagion, SEIZ
 7. [Network Robustness](): Power laws, preferential attachment
 8. [Network Evolution](): Densification, forest fire, temporal networks with PageRank
 9. [Knowledge Graphs and Metapaths](): Metapaths, reasoning and completion of KGs

network-methods/network-effects-and-cascading-behavior.md

@@ -0,0 +1,62 @@
+---
+layout: post
+title: Network Effects And Cascading Behaviour
+header-includes:
+   - \usepackage{amsmath}
+---
+
+In this section, we study how a infection propages through a network. We will look into two classed of model, namely decision based models and probabilistic models. But first lets look at some terminology used throughout the post.
+
+**Terminology**
+1. Cascade: Propagation tree created by spreading contagion
+2. Contagion: What is spreading in the network, e.g., diseases, tweet, etc.
+3. Infection: Adoption/activation of a node
+4. Main players: Infected/active nodes, early adopters
+
+# Decision Based Models
+In decision based models, every nodes independently decides whether to adopt the contagion or not depending upon its neighbors. The decision is modelled as a two-player coordination game between user and its neighbor and related payoffs. Hence a node with degree $$k$$ plays $$k$$ such games to decide its payoff and correspondingly its behavior.
+
+## Single Contagion Model
+There are two contagions $$A$$ and $$B$$ in the network and initially every node has behavior $$B$$. Every node can have only one behavior out of the two. The payoff matrix is given as:
+
+|   | A | B |
+|---|---|---|
+| A | a | 0 |
+| B | 0 | b |
+
+Lets analyze a node with d neighbors, and let p be the fraction of nodes who have adopted $$A$$. Hence the payoff for $$A$$ is $$apd$$ and payoff for $$B$$ is $$b(1-p)d$$. Hence the node adopts behavior $$A$$ if 
+$$apd > b(1-p)d \implies p > \frac{b}{a+b} = q$$(threshold)
+
+### Case Study: [Modelling Protest Recruitment on social networks](https://arxiv.org/abs/1111.5595)
+Key Insights:
+- Uniform activation threhold for users, with two peaks
+- Most cascades are short
+- Successful cascades are started by central users
+
+#### Note: 
+**k-core decomposition**: biggest connected subgraph where every node has at least degree k (iteratively remove nodes with degree less than k)
+
+### Multiple Contagion Model
+There are two contagions $$A$$ and $$B$$ in the network and initially every node has behavior $$B$$. In this case a node can have both behavior $$A$$ and $$B$$ at a total cost of $$c$$ (over all interactions). The payoff matrix is given as:
+
+|   | A | B | AB |
+|---|---|---|----|
+| A | a | 0 | a  |
+| B | 0 | b | b  |
+| AB| a | b | max(a,b)|
+
+### Example: Infinite Line graph 
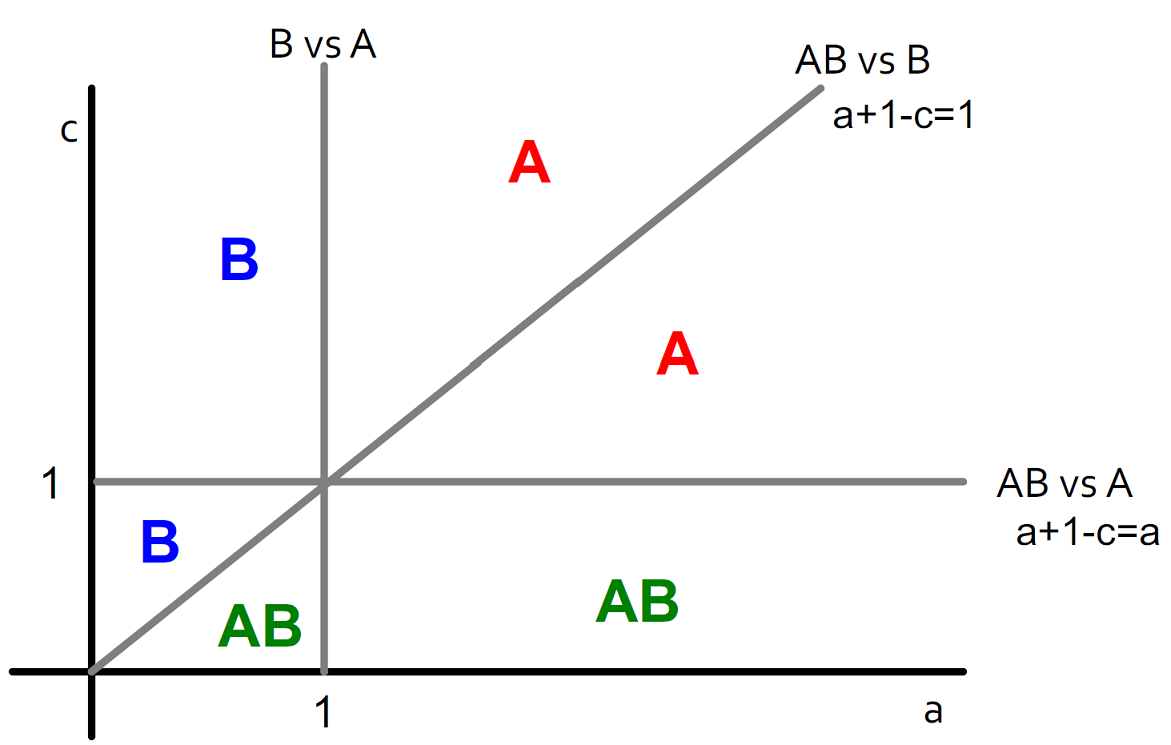
+**Case 1**:**A-w-B** 
+![decision_case_1](../assets/img/decision_model_1.png?style=centerme)
+
+Payoffs for $$w$$: $$A: a$$, $$B: 1$$, $$AB: a+1-c$$
+
+![decision_case_2](../assets/img/decision_model_2.png?style=centerme)
+
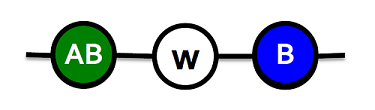
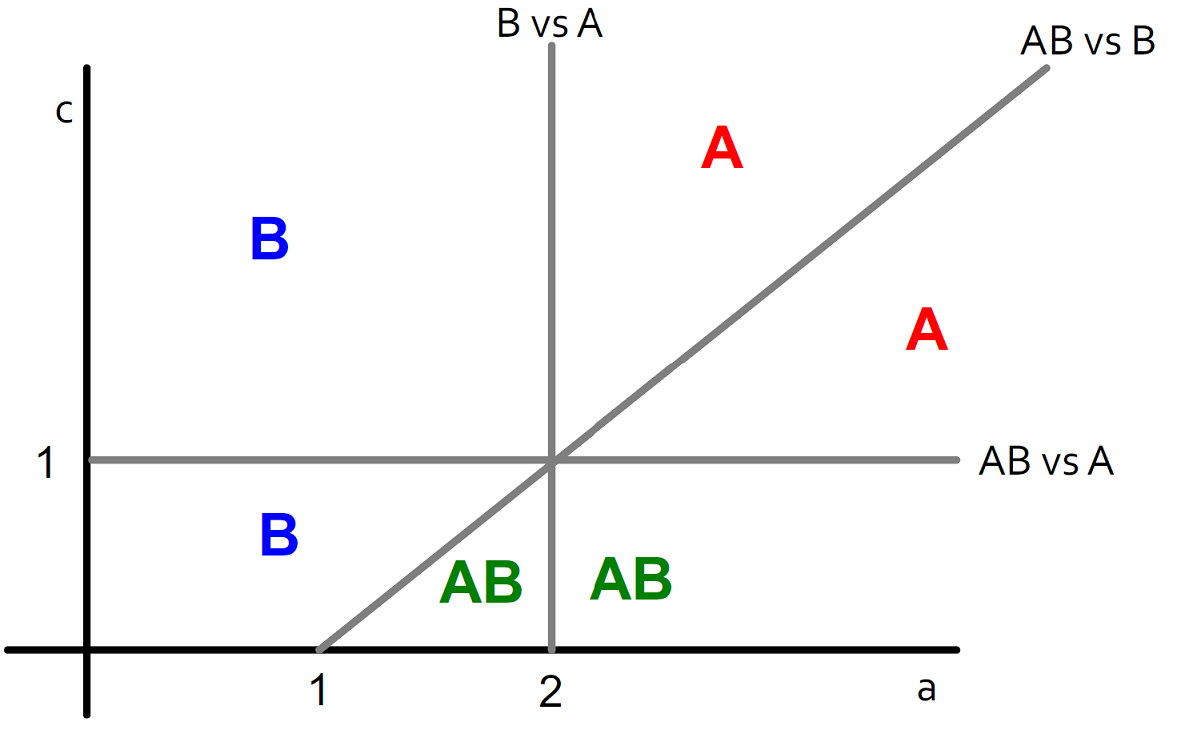
+**Case 1**: **AB-w-B**
+![decision_case_3](../assets/img/decision_model_3.png?style=centerme)
+
+Payoffs for $$w$$: $$A: a$$, $$B: 1$$, $$AB: max(a, 1) + 1 -c$$
+
+![decision_case_4](../assets/img/decision_model_4.png?style=centerme)
+