17 changed files with 763 additions and 0 deletions
Split View
Diff Options
-
BINblogContent/headerImages/asteroids.png
-
+763 -0blogContent/posts/data-science/developing-an-ai-to-play-asteroids-part-1.md
-
BINblogContent/posts/data-science/media/asteroids/2right.png
-
BINblogContent/posts/data-science/media/asteroids/4right.png
-
BINblogContent/posts/data-science/media/asteroids/5right.png
-
BINblogContent/posts/data-science/media/asteroids/GA200.png
-
BINblogContent/posts/data-science/media/asteroids/GA50.png
-
BINblogContent/posts/data-science/media/asteroids/GAvsRandom.png
-
BINblogContent/posts/data-science/media/asteroids/code.png
-
BINblogContent/posts/data-science/media/asteroids/dqn_after.png
-
BINblogContent/posts/data-science/media/asteroids/dqn_before.png
-
BINblogContent/posts/data-science/media/asteroids/randomSeed.png
-
BINblogContent/posts/data-science/media/asteroids/reflexPerformance.png
-
BINblogContent/posts/data-science/media/asteroids/reward.png
-
BINblogContent/posts/data-science/media/asteroids/reward_projection.png
-
BINblogContent/posts/data-science/media/asteroids/reward_trendline.png
-
BINblogContent/posts/data-science/media/asteroids/starting.png
BIN
blogContent/headerImages/asteroids.png
View File
+ 763
- 0
blogContent/posts/data-science/developing-an-ai-to-play-asteroids-part-1.md
View File
| @ -0,0 +1,763 @@ | |||
| I worked on this project during Dr. Homans's RIT CSCI-331 class. | |||
| # Introduction | |||
| This project explores the beautiful and frustrating ways in which we | |||
| can use AI to develop systems to solve problems. Asteroids is a | |||
| perfect example of a fun learning AI problem because Asteroids is | |||
| difficult for humans to play and has open-source frameworks that can | |||
| emulate the environment. Using the Open AI gym framework we developed | |||
| different AI agents to play Asteroids using various heuristics and ML | |||
| techniques. We then created a testbed to run experiments that | |||
| determine statistically whether our custom agents out-performs the | |||
| random agent. | |||
| # Methods and Results | |||
| Three agents were developed to play Asteroids. This report is broken | |||
| into segments where each agent is explained and its performance is | |||
| analyzed. | |||
| # Random Agent | |||
| The random agent simple takes a random action defined by the action | |||
| space. The resulting agent will randomly spin around and shoot | |||
| asteroids. Although this random agent is easy to implement, it is | |||
| ineffective because moving spastically will cause you to crash into | |||
| asteroids. Using this as the baseline for our performance, we can use | |||
| this random agent to access whether our agents are better than random | |||
| key smashing -- which is my strategy for playing Smash. | |||
| ```python | |||
| """ | |||
| ACTION_MEANING = { | |||
| 0: "NOOP", | |||
| 1: "FIRE", | |||
| 2: "UP", | |||
| 3: "RIGHT", | |||
| 4: "LEFT", | |||
| 5: "DOWN", | |||
| 6: "UPRIGHT", | |||
| 7: "UPLEFT", | |||
| 8: "DOWNRIGHT", | |||
| 9: "DOWNLEFT", | |||
| 10: "UPFIRE", | |||
| 11: "RIGHTFIRE", | |||
| 12: "LEFTFIRE", | |||
| 13: "DOWNFIRE", | |||
| 14: "UPRIGHTFIRE", | |||
| 15: "UPLEFTFIRE", | |||
| 16: "DOWNRIGHTFIRE", | |||
| 17: "DOWNLEFTFIRE", | |||
| } | |||
| """ | |||
| def act(self, observation, reward, done): | |||
| return self.action_space.sample() | |||
| ``` | |||
| ## Test on the Environment Seed | |||
| It is always important to know how randomness affects the results of | |||
| your experiment. In this agent, there are two sources of | |||
| randomness, the first being the seed given for the Gym environment and | |||
| the other is in the random function used to select a random action. By | |||
| default, the seed of the Gym library is set to zero. This is useful | |||
| for testing because if your agent is deterministic, you will always | |||
| get the same results. We can seed the environment with the current | |||
| time to add more randomness. However, this begs the question: to what | |||
| extent does the added randomness change the scores of the game. | |||
| Certain seeds in the Gym environment may make the game much | |||
| easier/harder to play thus altering the distribution of the score. | |||
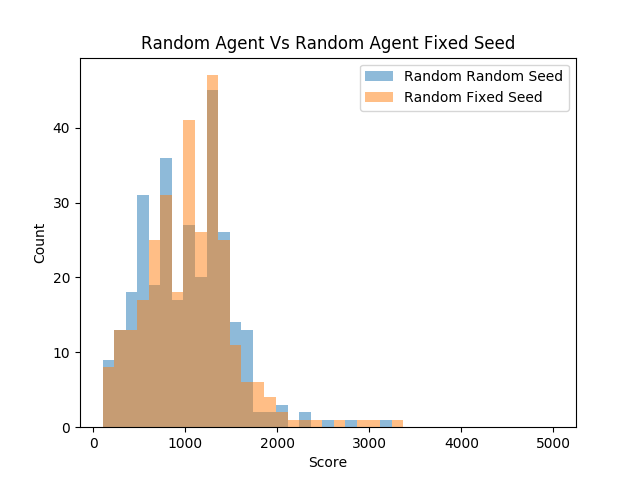
| A test was derived to compare the scores of the environment in both a | |||
| fixed seed and a time set seed. 300 trials of the random agent were ran | |||
| in both types of seeded environments. | |||
|  | |||
| ``` | |||
| Random Agent Time Seed: | |||
| mean:1005.6333333333333 | |||
| max:3220.0 | |||
| min:110.0 | |||
| sd:478.32548077178114 | |||
| median:980.0 n:300 | |||
| Random Agent Fixed Seed: | |||
| mean:1049.3666666666666 | |||
| max:3320.0 | |||
| min:110.0 | |||
| sd:485.90321281323327 | |||
| median:1080.0 | |||
| n:300 | |||
| ``` | |||
| What is astonishing is that both distributions are nearly identical in | |||
| every way. Although the means are slightly different, there appears to | |||
| be no apparent difference between the distributions of scores. One | |||
| might expect that having more randomness would at least change the | |||
| variance of the scores, but none of that has happened. | |||
| ``` | |||
| Random agent vs Random fixed seed | |||
| F_onewayResult( | |||
| statistic=1.2300971733588375, | |||
| pvalue=0.2678339696597312 | |||
| ) | |||
| ``` | |||
| With such a high p-value we can not reject the null hypothesis that | |||
| these distributions are statistically different. This is a powerful | |||
| conclusion to come to because it allows us to run future experiments | |||
| understanding that a specific seed on average will not have a | |||
| statistically significant impact on the performance of a random agent. | |||
| However, this finding does not help us understand the impact that the | |||
| seed has on a fully deterministic agent. It is still possible that a | |||
| fully deterministic system will have varying scores on different | |||
| environment seeds. | |||
| # Reflex Agent | |||
| Our reflex agent observes the environment and decides what to do based | |||
| on a simple rule set. The reflex agent is broken into three sections: | |||
| feature extraction, reflex rules, and performance. | |||
| ## Feature Extraction | |||
| The largest part of this agent was devoted to parsing the environment | |||
| into a more usable form. The feature extraction for this project was | |||
| rather difficult since the environment was given as a pixel array and | |||
| the screen flashed the asteroids and then the player. Trying to | |||
| achieve the best performance with the minimal amount of algorithmic | |||
| engineering, this reflex agent parsed 3 things from the environment: | |||
| position, direction, closest asteroid. | |||
| ### 1: Player Position | |||
| Finding the position of the player was relatively easy since you only | |||
| had to scan the environment to find pixels of certain RGB values. To | |||
| account for the flashing environment, you would just store the | |||
| position in the fields of the class so that it is persistent between | |||
| action loops. The position of the player would only be updated if a | |||
| new player is observed. | |||
| ```python | |||
| AGENT_RGB = [240, 128, 128] | |||
| ``` | |||
| ### 2: Player Direction | |||
| Detecting the position of the player could be made difficult if you | |||
| were only going off the RGB values of the player. Although when the | |||
| player is upright, it is straight forward, when the player is sideways | |||
| things get super difficult. | |||
| ```python | |||
| action_sequence = [3,3,3,3,3,0, 0,0] | |||
| class Agent(object): | |||
| def __init__(self, action_space): | |||
| self.action_space = action_space | |||
| # Defines how the agent should act | |||
| def act(self, observation, reward, done): | |||
| if len(action_sequence) > 0: | |||
| action = action_sequence[0] | |||
| action_sequence.remove(action) | |||
| return action | |||
| return 0 | |||
| ``` | |||
|  | |||
|  | |||
|  | |||
| We created a basic script to observe what the player does when given a | |||
| specific sequence of actions. I was pleased to notice that exactly 5 | |||
| turns to the left/right correlated to a perfect 90 degrees. By keeping | |||
| track of our current rotation according to the actions that we have | |||
| taken, we can precisely keep track of our current rotational direction | |||
| without parsing the horrendous pixel array when the player is | |||
| sideways. | |||
| ### 3: Position of Closest Asteroid | |||
| Asteroids were detected as being any pixel that was not empty (0,0,0) | |||
| and not the player (240, 128, 128). Using a simple single pass through | |||
| the environment matrix, we were able to detect the closest asteroid to | |||
| the latest known position of the player. | |||
| ## Agent Reflex | |||
| Based on my actual strategy for asteroids, this agent stays in the | |||
| middle of the screen and shoots at the closest asteroid to it. | |||
| ```python | |||
| def act(self, observation, reward, done): | |||
| observation = np.array(observation) | |||
| self.updateState(observation) | |||
| dirOfAstroid = math.atan2(self.closestRow-self.row, self.closestCol- self.col) | |||
| dirOfAstroid = self.deWarpAngle(dirOfAstroid) | |||
| self.shotLast = not self.shotLast | |||
| if self.shotLast: | |||
| return 1 # fire | |||
| if self.currentDirection - dirOfAstroid < 0: | |||
| self.updateDirection(math.pi/10) | |||
| if self.shotLast: | |||
| return 12 # left fire | |||
| return 4 # left | |||
| else: | |||
| self.updateDirection(-1*math.pi/10) | |||
| return 3 # right | |||
| ``` | |||
| Despite being a simple agent, this performs well since it can shoot at asteroids before it hits them. | |||
| ## Results of Reflex Agent | |||
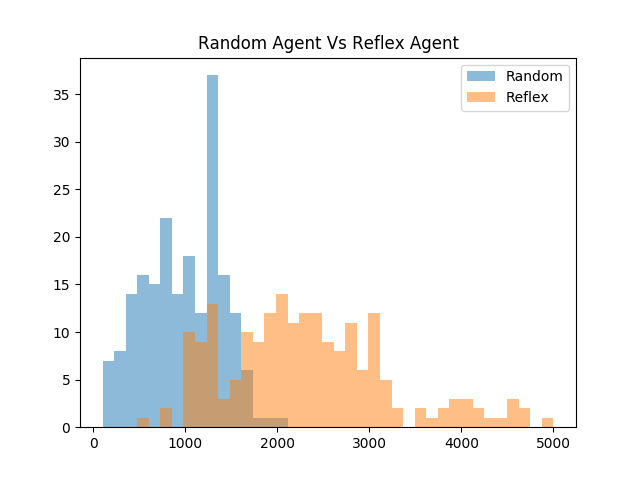
| In this trial, 200 tests of both the random agent and the reflex agent | |||
| were observed while setting the seed of the environment to the current | |||
| time. The seed was randomly set in this scenario since the reflex | |||
| agent is fully deterministic and would perform identically in each trial | |||
| otherwise. | |||
|  | |||
| The histogram depicts that the reflex agent on average performs | |||
| significantly better than the random agent. What is fascinating to | |||
| note is that even though the agent's actions are deterministic, the | |||
| seed of the environment created a large amount of variance in the | |||
| scores observed. It is arguably misleading to only provide a single | |||
| score for an agent as its performance because the environment seed has | |||
| a large impact on the non-random agent's scores. | |||
| ``` | |||
| Reflex Agent: | |||
| mean:2385.25 | |||
| max:8110.0 | |||
| min:530.0 | |||
| sd:1066.217115553863 | |||
| median:2250.0 | |||
| n:200 | |||
| Random Agent: | |||
| mean:976.15 | |||
| max:2030.0 | |||
| min:110.0 | |||
| sd:425.2712987023695 | |||
| median:980.0 | |||
| n:200 | |||
| ``` | |||
| One thing that is interesting about comparing the two distributions is | |||
| that the reflex agent has a much larger standard deviation in its | |||
| scores than the random agent. It is also interesting to note that the | |||
| reflex agent's worst performance was significantly better than the | |||
| random agent's worst performance. Also, the best performance of the | |||
| reflex agent shatters the best performance of the random agent. | |||
| ``` | |||
| Random agent vs reflex | |||
| F_onewayResult( | |||
| statistic=299.86689786081956, | |||
| pvalue=1.777062051091977e-50 | |||
| ) | |||
| ``` | |||
| Since we took such a sample size of two hundred, and the populations | |||
| were significantly different, we got a p score of nearly zero | |||
| (1.77e-50). With a p-value like this, we can say with nearly 100% | |||
| confidence (with rounding) that these two populations are different | |||
| and that the reflex agent out-performs the random agent. | |||
| # Genetic Algorithm | |||
| Genetic algorithms employ the same tactics used in natural selection | |||
| to find an optimal solution to an optimization problem. Genetic | |||
| algorithms are often used in high dimensional problems where the | |||
| optimal solutions are not apparent. Genetic algorithms are commonly | |||
| used to tune the hyper-parameters of a program. However, this | |||
| algorithm can be used in any scenario where you have a function that | |||
| defines how well a solution is. | |||
| In the scenario of asteroids, we can employ genetic algorithms to find | |||
| the optimal sequence of moves to make to achieve the highest score | |||
| possible. The chromosomes are well defined as the sequence of actions | |||
| to loop through and the fitness function is simply the score that the | |||
| agent achieves. | |||
| ## Algorithm Implementation | |||
| The actual implementation of the genetic algorithm was pretty straight | |||
| forward, the agent simply looped through a sequence of events where | |||
| each event represents a gene on the chromosome. | |||
| ```python | |||
| class Agent(object): | |||
| """Very Basic GA Agent""" | |||
| def __init__(self, action_space, chromosome): | |||
| self.action_space = action_space | |||
| self.chromosome = chromosome | |||
| self.index = 0 | |||
| # You should modify this function | |||
| def act(self, observation, reward, done): | |||
| if self.index >= len(self.chromosome)-1: | |||
| self.index = 0 | |||
| else: | |||
| self.index = self.index + 1 | |||
| return self.chromosome[self.index] | |||
| ``` | |||
| Rather than using a library, a simple home-brewed genetic algorithm | |||
| was created from scratch. The basic algorithm essentially is in a loop | |||
| that runs functions necessary to iterate through each generation. | |||
| Each generation can be broken apart into a few steps: | |||
| - selection: removes the worst-performing chromosomes | |||
| - mating: uses crossover to create new chromosomes | |||
| - mutation: adds randomness to the chromosome | |||
| - fitness: evaluates the performance of each chromosome | |||
| In roughly 100 lines of python, a basic genetic algorithm was crafted. | |||
| ```python | |||
| AVAILABLE_COMMANDS = [0,1,2,3,4] | |||
| def generateRandomChromosome(chromosomeLength): | |||
| chrom = [] | |||
| for i in range(0, chromosomeLength): | |||
| chrom.append(choice(AVAILABLE_COMMANDS)) | |||
| return chrom | |||
| """ | |||
| creates a random population | |||
| """ | |||
| def createPopulation(populationSize, chromosomeLength): | |||
| pop = [] | |||
| for i in range(0, populationSize): | |||
| pop.append((0,generateRandomChromosome(chromosomeLength))) | |||
| return pop | |||
| """ | |||
| computes fitness of population and sorts the array based | |||
| on fitness | |||
| """ | |||
| def computeFitness(population): | |||
| for i in range(0, len(population)): | |||
| population[i] = (calculatePerformance(population[i][1]), population[i][1]) | |||
| population.sort(key=lambda tup: tup[0], reverse=True) # sorts population in place | |||
| """ | |||
| kills the weakest portion of the population | |||
| """ | |||
| def selection(population, keep): | |||
| origSize = len(population) | |||
| for i in range(keep, origSize): | |||
| population.remove(population[keep]) | |||
| """ | |||
| Uses crossover to mate two chromosomes together. | |||
| """ | |||
| def mateBois(chrom1, chrom2): | |||
| pivotPoint = randrange(len(chrom1)) | |||
| bb = [] | |||
| for i in range(0, pivotPoint): | |||
| bb.append(chrom1[i]) | |||
| for i in range(pivotPoint, len(chrom2)): | |||
| bb.append(chrom1[i]) | |||
| return (0, bb) | |||
| """ | |||
| brings population back up to desired size of population | |||
| using crossover mating | |||
| """ | |||
| def mating(population, populationSize): | |||
| newBlood = populationSize - len(population) | |||
| newbies = [] | |||
| for i in range(0, newBlood): | |||
| newbies.append(mateBois(choice(population)[1], | |||
| choice(population)[1])) | |||
| population.extend(newbies) | |||
| """ | |||
| Randomly mutates x chromosomes -- excluding best chromosome | |||
| """ | |||
| def mutation(population, mutationRate): | |||
| changes = random() * mutationRate * len(population) * len(population[0][1]) | |||
| for i in range(0, int(changes)): | |||
| ind = randrange(len(population) -1) + 1 | |||
| chrom = randrange(len(population[0][1])) | |||
| population[ind][1][chrom] = choice(AVAILABLE_COMMANDS) | |||
| """ | |||
| Computes average score of population | |||
| """ | |||
| def computeAverageScore(population): | |||
| total = 0.0 | |||
| for c in population: | |||
| total = total + c[0] | |||
| return total/len(population) | |||
| def runGeneration(population, populationSize, keep, mutationRate): | |||
| selection(population, keep) | |||
| mating(population, populationSize) | |||
| mutation(population, mutationRate) | |||
| computeFitness(population) | |||
| """ | |||
| Runs the genetic algorithm | |||
| """ | |||
| def runGeneticAlgorithm(populationSize, maxGenerations, | |||
| chromosomeLength, keep, mutationRate): | |||
| population = createPopulation(populationSize, chromosomeLength) | |||
| best = [] | |||
| average = [] | |||
| generations = range(1, maxGenerations + 1) | |||
| for i in range(1, maxGenerations + 1): | |||
| print("Generation: " + str(i)) | |||
| runGeneration(population, populationSize, keep, mutationRate) | |||
| a = computeAverageScore(population) | |||
| average.append(a) | |||
| best.append(population[0][0]) | |||
| print("Best Score: " + str(population[0][0])) | |||
| print("Average Score: " + str(a)) | |||
| print("Best chromosome: " + str(population[0][1])) | |||
| print() | |||
| pyplot.plot(generations, best, color='g', label='Best') | |||
| pyplot.plot(generations, average, color='orange', label='Average') | |||
| pyplot.xlabel("Generations") | |||
| pyplot.ylabel("Score") | |||
| pyplot.title("Training GA Algorithm") | |||
| pyplot.legend() | |||
| pyplot.show() | |||
| ``` | |||
| ## Results | |||
|  | |||
|  | |||
| ``` | |||
| Generation: 200 | |||
| Best Score: 8090.0 | |||
| Average Score: 2492.6666666666665 | |||
| Best chromosome: [1, 4, 1, 4, 4, 1, 0, 4, 2, 4, 1, 3, 2, 0, 2, 0, 0, 1, 3, 0, 1, 0, 4, 0, 1, 4, 1, 2, 0, 1, 3, 1, 3, 1, 3, 1, 0, 4, 4, 1, 3, 4, 1, 1, 2, 0, 4, 3, 3, 0] | |||
| ``` | |||
| It is impressive that a simple genetic algorithm can learn how | |||
| to perform well when the seed is fixed. When compared to the | |||
| random agent which had a max score of 3320 with a fixed seed, the | |||
| optimized genetic algorithm shattered the random agents' best | |||
| performance by a factor of 2.5. | |||
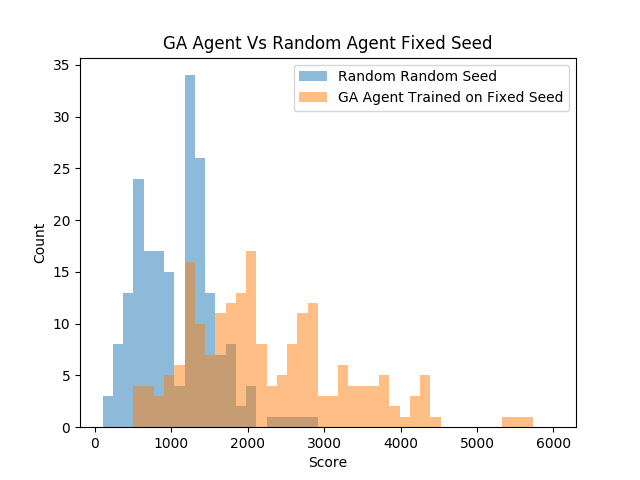
| Since we trained an optimized set of actions to take to achieve a high | |||
| score on a specific seed, what would happen if we randomized the seed? | |||
| A test was conducted to compare the trained GA agent with 200 | |||
| generations against the random agent. For both agents, the seed was | |||
| randomized by setting it to the current time. | |||
|  | |||
| ``` | |||
| GA Performance Trained on Fixed Seed: | |||
| mean:2257.9 | |||
| max:5600.0 | |||
| min:530.0 | |||
| sd:1018.4363455808125 | |||
| median:2020.0 | |||
| n:200 | |||
| ``` | |||
| ``` | |||
| Random Random Seed: | |||
| mean:1079.45 | |||
| max:2800.0 | |||
| min:110.0 | |||
| sd:498.9340612746338 | |||
| median:1080.0 | |||
| n:200 | |||
| ``` | |||
| ``` | |||
| F_onewayResult( | |||
| statistic=214.87432376234608, | |||
| pvalue=3.289638100969386e-39 | |||
| ) | |||
| ``` | |||
| As expected, the GA agent did not perform as well on random seeds as | |||
| it did on the fixed seed that it was trained on. However, the GA was | |||
| able to find an action sequence that statistically beat the random | |||
| agent as observed in the score distributions above and the extremely | |||
| small p-value. Although luck was a part of getting the agent to get a | |||
| score of 8k on the seed of zero, the skill that it learned was | |||
| somewhat applicable to other seeds. After replaying the video of the | |||
| agent play, it just slowly drifts around the screen and shoots at | |||
| asteroids in front of it. This has a major advantage over the random | |||
| agent since the random agent tends to move very fast and rotate | |||
| spastically. | |||
| ## Future Work | |||
| This algorithm was more or less a last-minute hack to see if I can | |||
| make a cool video of a high scoring asteroids agent. Future agents | |||
| using genetic algorithms would incorporate reflex to dynamically | |||
| respond to the environment. Based on which direction asteroids are in | |||
| proximity to the player, the agent could select a different chromosome | |||
| of actions to execute. This would potentially yield scores above ten thousand if trained and implemented correctly. Future training | |||
| should also incorporate randomness to the seed so that the skills | |||
| learned are the most transferable to other random environments. | |||
| # Deep Q-Learning Agent | |||
| ## Introduction: | |||
| The inspiration behind attempting a reinforcement learning agent for | |||
| this problem scope is the original DQN paper that came out from | |||
| Deepmind, “Playing Atari with Deep Reinforcement Learning.” This paper | |||
| showed the potential of utilizing this Deep Q-learning methodology on | |||
| a variety of simulated Atari games using one standardized architecture | |||
| across all. Reinforcement learning has always been of interest and to | |||
| have the opportunity to spend time learning about it while applying | |||
| for a class setting was exciting, even if it is out of the scope of | |||
| the class presently. It has been an exciting challenge to read through | |||
| and implement a research paper to get similar results. | |||
| Deep Q-Learning is an extension of the standard Q-Learning algorithm | |||
| in which a neural network is used to approximate the optimal | |||
| action-value function, Q\*(s,a). The action-value function is the | |||
| function that outputs the expected maximum reward given a state and a | |||
| policy mapping to actions or distributions of actions. Logically, this | |||
| works as the Q function follows the Bellman equation identity, which | |||
| states that if the optimal action for the next step state is known, | |||
| then the optimal output given an action a’ follows by maximizing the | |||
| expected reward of the equation, r+Q*(s',a'). Thus, the reinforcement | |||
| learning part comes in the form of a neural network approximating the | |||
| optimal action-value function by using the Bellman equation identity | |||
| as an iterative update at every time step. | |||
| ## Agent architecture: | |||
| The basis of the network architecture is a basic convolutional network | |||
| with 2 conv layers, a fully connected layer, and then an output layer | |||
| of 14 classes with each representing an individual action. The first | |||
| layer consists of 16 8x8 filters and takes a stride 4 while the second | |||
| has 32 4x4 filters and only takes a stride of 2. Following this layer, | |||
| the filters are compressed into a 1-D representation vector of size | |||
| 12,672 that’s passed through a fully connected layer of 256 nodes. | |||
| All layers sans the output layer are activated using the ReLU function. | |||
| The optimization algorithm of choice was the Adam optimizer, using a | |||
| learning rate equal to .0001 and default betas of [.9, .99]. The | |||
| discount factor, or gamma, related to future expected rewards was set | |||
| at .99 and the probability of taking a random action per action step | |||
| was linearly annealed from 1.0 down to a fixed .1 after one million | |||
| seen frames. | |||
|  | |||
| ## Experience Replay: | |||
| One of the main points within the original paper that significantly | |||
| helped the training of this network is the introduction of a Replay | |||
| Buffer that is used during the training. To break all the | |||
| temporal correlation between sequential frames and biasing the | |||
| training of a network-based off certain chains of situations, a | |||
| historical buffer of transitions is used to sample mini-batches to | |||
| train on per time step. Every time an action is made, a tuple | |||
| consisting of the current state, the action is taken, the reward gained, and | |||
| the subsequent state (s, a, r, s’) is stored into the buffer. And at | |||
| every training step, a mini-batch is sampled from the buffer and used | |||
| to train the network. This allows the network to be trained in | |||
| non-correlated transitions and hopefully train in a more generalized | |||
| way to the environment rather than biased to a string of similar | |||
| actions. | |||
| ## Preprocessing: | |||
| One of the first issues that had to be tackled was the issue of the | |||
| high dimensionality of the input image and how that information was | |||
| duplicated stored in the Replay Buffer. Each observation given from | |||
| the environment is a matrix of (210, 160, 3) pixels representing the | |||
| RGB pixels within the frame. For time and being | |||
| computationally efficient, it was needed to preprocess and reduce the | |||
| dimensionality of the observations as a single frame stack (of which | |||
| there are two per transition) consists of (4, 3, 210, 160) or 403,000 | |||
| input features that would have to be dealt with. | |||
|  | |||
| Firstly, images are converted into a grayscale image and the | |||
| reward/number lives section at the top of the screen is cut out since | |||
| it is irrelevant to the network’s vision. Furthermore, the now (4, | |||
| 192, 160) matrix was downsampled by taking every other pixel to (4, | |||
| 96, 80), resulting in a change from 403,000 input features to only | |||
| 30,720 - a substantial reduction in the calculations needed while | |||
| maintaining strong input information for the network. | |||
|  | |||
| ## Training: | |||
| Training for the bot was conducted by modifying the main function to | |||
| allow games to immediately start after one was finished, to | |||
| make continuous training of the agent easier. All the environment | |||
| parameters were reset and the temporary attributes of the agent (ie. | |||
| current state/next state) were flushed. For the first four frames of a | |||
| game, the bot just gathered a stack of frames. And following that, at | |||
| every time the next state was compiled and the transition tuple pushed | |||
| onto the buffer, as well as a training step for the agent. For the | |||
| training step, a random batch was grabbed from the replay buffer and | |||
| used to calculate the loss function between actual and expected | |||
| Q-values. This was used to calculate the gradients for the | |||
| backpropagation of the network. | |||
| ## Outcome: | |||
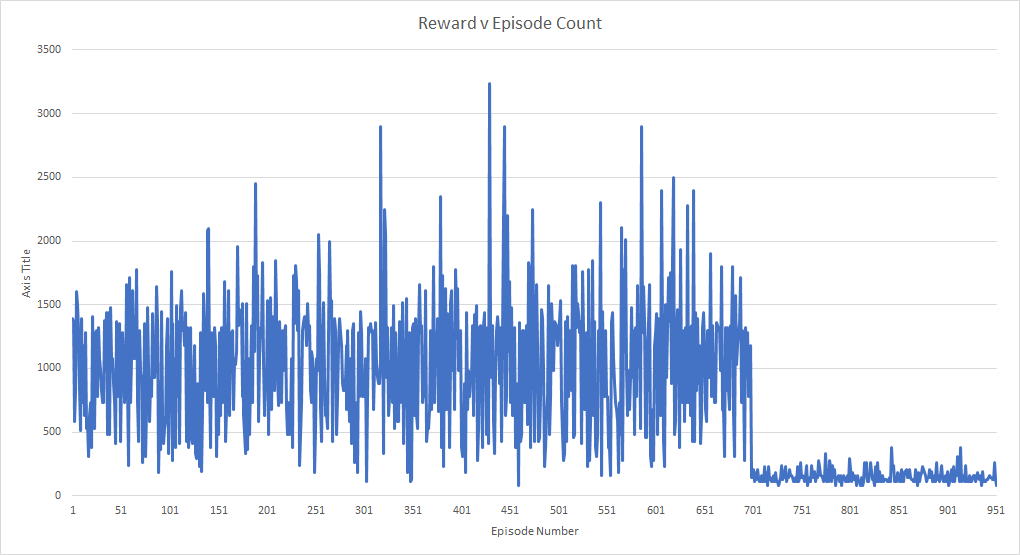
| Unfortunately, the result of 48 hours of continuous training, 950 | |||
| games played, and roughly 1.3 million frames of game footage seen, was | |||
| that the agent converged to a suicidal policy that resulted in a | |||
| consistent garbage performance. | |||
|  | |||
| The model transitioned to the fixed 90% model action chance around | |||
| episode 700, which is exactly where the agent starts to go awry. The | |||
| strange part about this is since the random action chance is linearly | |||
| annealed over the first million frames, if the agent had continuously | |||
| been following a garbage policy, it would’ve been expected that the | |||
| rewards would steadily decrease over time as the network takes more | |||
| control. | |||
|  | |||
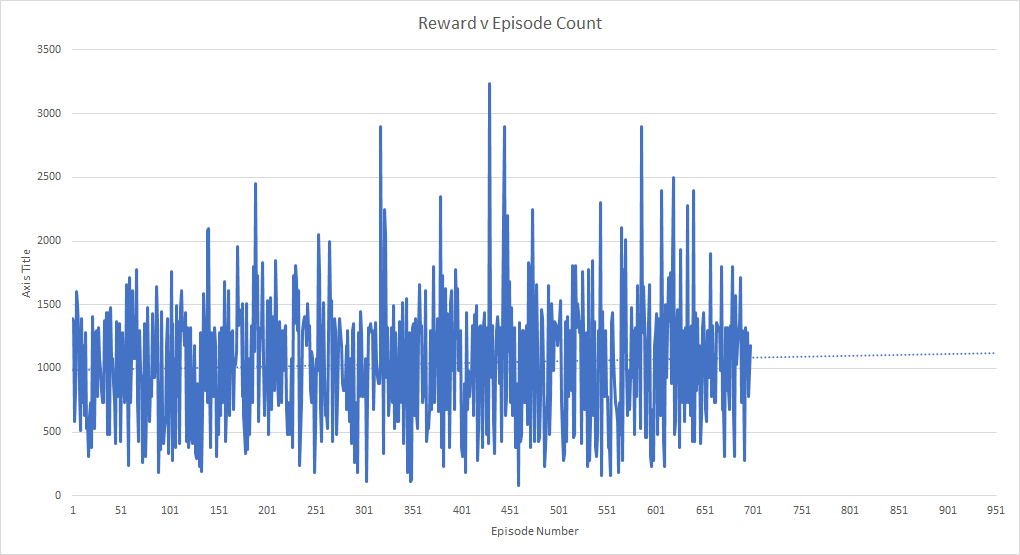
| Up until that point, the projection of the reward trendline was a | |||
| steady rise per the number of episodes. Expanding this out until | |||
| 10,000 frames (approximately 10 million frames seen, the same amount | |||
| of time the original Deepmind paper trained these bots for), the | |||
| projected score is in the realms of 2,400 to 2,500 - which matches up | |||
| closely to the well-tuned reflex agent and the GA agent on a random | |||
| seed. | |||
|  | |||
| It would’ve been exciting to see how the model compared to | |||
| our reflex agent had it been able to train consistently up until the | |||
| end. | |||
| ## Limitations: | |||
| There were a fair number of limitations that were present within the | |||
| execution and training of this model that possibly contributed to the | |||
| slow and unstable training of the network. Differences in the | |||
| algorithm from the original paper is that the optimization function | |||
| utilized was the Adam optimizer instead of RMSProp and the replay | |||
| buffer only took into consideration the previous 50k frames, not the | |||
| past one million. It might be possible that the weaker replay buffer | |||
| was to blame as the model was continuously fed a sub-optimal within | |||
| its past 50,000 frames that caused it to diverge so heavily near the | |||
| end. | |||
| One issue in preprocessing that might've led the bot astray is using | |||
| not using the max pixelwise combination between sequential frames in | |||
| order to have each frame include both the asteroids and the player. | |||
| Since the Atari (and by extension, this environment simulation) | |||
| doesn't render the asteroids and the player sprite all in the same | |||
| frame, it is possible that the network was unable to extract any | |||
| coherent connection between the alternating frames. | |||
| Regarding optimizations built on the DQN algorithm past the original | |||
| Deepmind paper, we did not use a policy and a target network in | |||
| training. In the original algorithm, the estimation and attempt at | |||
| converging to the target policy is unstable due to the target | |||
| network’s weights continuously shifting during training. For the | |||
| network, it’s hard to converge to something that’s continually | |||
| shifting at every time step and leads to very noisy and unstable | |||
| training. One optimization that has been proposed for DQN is to have a | |||
| policy and target network. At every timestep, the policy network’s | |||
| weights are updated with the calculated gradients while the target | |||
| network is maintained for a number of steps. This lets the target | |||
| policy be still for a few time steps while the network is converging | |||
| to it and leads to more stable and guided training. | |||
| Perhaps the largest limitation in training was the computational power | |||
| used for training. The network was trained on a single GTX1060ti GPU, | |||
| which led to just single episodes taking a few minutes to complete. It | |||
| would’ve taken an incredibly long time to hit 10 million seen frames | |||
| as even just 1.3 million took approximately 48 hours. It’s probable | |||
| that our implementation is inefficient in its calculations, however it | |||
| is a well known limitation of RL that it is time and computationally | |||
| intensive. | |||
| ## Deep Q Conclusions: | |||
| This was a fun agent and algorithm to implement, even if at present it | |||
| has given little to no results back in terms of performance. The plan | |||
| is to continue testing and training the agent, even after the | |||
| deadline. Reinforcement learning is a complicated and hard to debug | |||
| environment, but similarly an exciting challenge due to its potential | |||
| for solving and overcoming problems. | |||
| # Conclusion | |||
| This project demonstrated how fun it can be to train AI agents to play | |||
| video games. Although none of our agents are earth-shatteringly | |||
| amazing, we were able to use statistical measures to determine that | |||
| the reflex and GA agents outperformed the random agent. The GA agent | |||
| and the convolutional neural network show very promising and future | |||
| work can be used to drastically improve their results. | |||