Added asteroids project to the blog

blogContent/posts/data-science/developing-an-ai-to-play-asteroids-part-1.md

@@ -0,0 +1,763 @@
+I worked on this project during Dr. Homans's RIT CSCI-331 class.
+
+# Introduction
+
+This project explores the beautiful and frustrating ways in which we
+can use AI to develop systems to solve problems. Asteroids is a
+perfect example of a fun learning AI problem because Asteroids is
+difficult for humans to play and has open-source frameworks that can
+emulate the environment. Using the Open AI gym framework we developed
+different AI agents to play Asteroids using various heuristics and ML
+techniques.  We then created a testbed to run experiments that
+determine statistically whether our custom agents out-performs the
+random agent.
+
+
+# Methods and Results
+
+Three agents were developed to play Asteroids. This report is broken
+into segments where each agent is explained and its performance is
+analyzed. 
+
+# Random Agent
+
+The random agent simple takes a random action defined by the action
+space. The resulting agent will randomly spin around and shoot
+asteroids. Although this random agent is easy to implement, it is
+ineffective because moving spastically will cause you to crash into
+asteroids.  Using this as the baseline for our performance, we can use
+this random agent to access whether our agents are better than random
+key smashing -- which is my strategy for playing Smash. 
+
+
+```python
+"""
+ACTION_MEANING = {
+    0: "NOOP",
+    1: "FIRE",
+    2: "UP",
+    3: "RIGHT",
+    4: "LEFT",
+    5: "DOWN",
+    6: "UPRIGHT",
+    7: "UPLEFT",
+    8: "DOWNRIGHT",
+    9: "DOWNLEFT",
+    10: "UPFIRE",
+    11: "RIGHTFIRE",
+    12: "LEFTFIRE",
+    13: "DOWNFIRE",
+    14: "UPRIGHTFIRE",
+    15: "UPLEFTFIRE",
+    16: "DOWNRIGHTFIRE",
+    17: "DOWNLEFTFIRE",
+}
+"""
+def act(self, observation, reward, done):
+    return self.action_space.sample()
+```
+
+## Test on the Environment Seed
+
+It is always important to know how randomness affects the results of
+your experiment. In this agent, there are two sources of
+randomness, the first being the seed given for the Gym environment and
+the other is in the random function used to select a random action. By
+default, the seed of the Gym library is set to zero. This is useful
+for testing because if your agent is deterministic, you will always
+get the same results. We can seed the environment with the current
+time to add more randomness. However, this begs the question: to what
+extent does the added randomness change the scores of the game. 
+Certain seeds in the Gym environment may make the game much
+easier/harder to play thus altering the distribution of the score. 
+
+
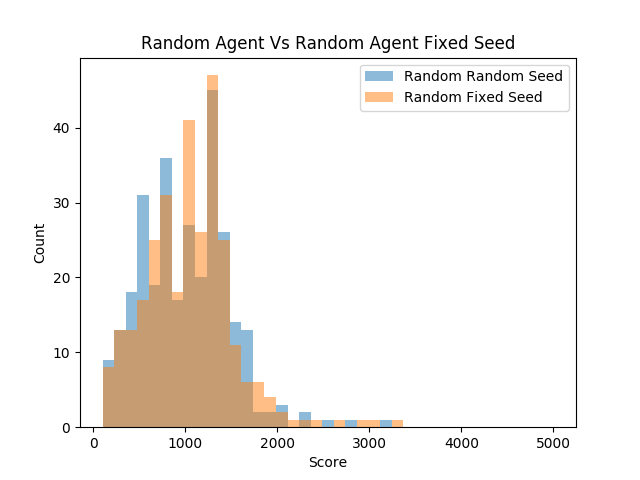
+A test was derived to compare the scores of the environment in both a
+fixed seed and a time set seed. 300 trials of the random agent were ran
+in both types of seeded environments. 
+
+![Seed Effect](media/asteroids/randomSeed.png)
+
+
+```
+Random Agent Time Seed: 
+    mean:1005.6333333333333 
+    max:3220.0 
+    min:110.0 
+    sd:478.32548077178114 
+    median:980.0 n:300
+
+Random Agent Fixed Seed: 
+    mean:1049.3666666666666 
+    max:3320.0 
+    min:110.0 
+    sd:485.90321281323327 
+    median:1080.0 
+    n:300
+```
+
+What is astonishing is that both distributions are nearly identical in
+every way. Although the means are slightly different, there appears to
+be no apparent difference between the distributions of scores. One
+might expect that having more randomness would at least change the
+variance of the scores, but none of that has happened.
+
+```
+Random agent vs Random fixed seed
+F_onewayResult(
+    statistic=1.2300971733588375, 
+    pvalue=0.2678339696597312
+)
+```
+
+With such a high p-value we can not reject the null hypothesis that
+these distributions are statistically different. This is a powerful
+conclusion to come to because it allows us to run future experiments
+understanding that a specific seed on average will not have a
+statistically significant impact on the performance of a random agent.
+However, this finding does not help us understand the impact that the
+seed has on a fully deterministic agent. It is still possible that a
+fully deterministic system will have varying scores on different
+environment seeds. 
+
+
+# Reflex Agent
+
+Our reflex agent observes the environment and decides what to do based
+on a simple rule set. The reflex agent is broken into three sections:
+feature extraction, reflex rules, and performance. 
+
+## Feature Extraction
+
+The largest part of this agent was devoted to parsing the environment
+into a more usable form. The feature extraction for this project was
+rather difficult since the environment was given as a pixel array and
+the screen flashed the asteroids and then the player. Trying to
+achieve the best performance with the minimal amount of algorithmic
+engineering, this reflex agent parsed 3 things from the environment:
+position, direction, closest asteroid. 
+
+
+### 1: Player Position
+
+Finding the position of the player was relatively easy since you only
+had to scan the environment to find pixels of certain RGB values. To
+account for the flashing environment, you would just store the
+position in the fields of the class so that it is persistent between
+action loops. The position of the player would only be updated if a
+new player is observed. 
+
+```python
+AGENT_RGB = [240, 128, 128] 
+```
+
+### 2: Player Direction
+
+Detecting the position of the player could be made difficult if you
+were only going off the RGB values of the player. Although when the
+player is upright, it is straight forward, when the player is sideways
+things get super difficult. 
+
+
+```python
+action_sequence = [3,3,3,3,3,0, 0,0]
+
+class Agent(object):
+    def __init__(self, action_space):
+        self.action_space = action_space
+
+    # Defines how the agent should act
+    def act(self, observation, reward, done):
+        if len(action_sequence) > 0:
+            action = action_sequence[0]
+            action_sequence.remove(action)
+            return action
+        return 0
+```
+
+![Starting Position](media/asteroids/starting.png)
+
+
+![4 Turns Right](media/asteroids/4right.png)
+
+
+![5 Turns Right](media/asteroids/5right.png)
+
+
+We created a basic script to observe what the player does when given a
+specific sequence of actions. I was pleased to notice that exactly 5
+turns to the left/right correlated to a perfect 90 degrees. By keeping
+track of our current rotation according to the actions that we have
+taken, we can precisely keep track of our current rotational direction
+without parsing the horrendous pixel array when the player is
+sideways. 
+
+
+### 3: Position of Closest Asteroid
+
+Asteroids were detected as being any pixel that was not empty (0,0,0)
+and not the player (240, 128, 128). Using a simple single pass through
+the environment matrix, we were able to detect the closest asteroid to
+the latest known position of the player.
+
+## Agent Reflex
+
+Based on my actual strategy for asteroids, this agent stays in the
+middle of the screen and shoots at the closest asteroid to it. 
+
+```python
+def act(self, observation, reward, done):
+    observation = np.array(observation)
+    self.updateState(observation)
+    dirOfAstroid = math.atan2(self.closestRow-self.row, self.closestCol- self.col)
+
+    dirOfAstroid = self.deWarpAngle(dirOfAstroid)
+
+    self.shotLast = not self.shotLast
+    if self.shotLast:
+        return 1 # fire
+    if self.currentDirection - dirOfAstroid < 0:
+        self.updateDirection(math.pi/10)
+        if self.shotLast:
+            return 12 # left fire
+        return 4 # left
+    else:
+        self.updateDirection(-1*math.pi/10)
+        return 3 # right
+```
+
+Despite being a simple agent, this performs well since it can shoot at asteroids before it hits them. 
+
+## Results of Reflex Agent
+
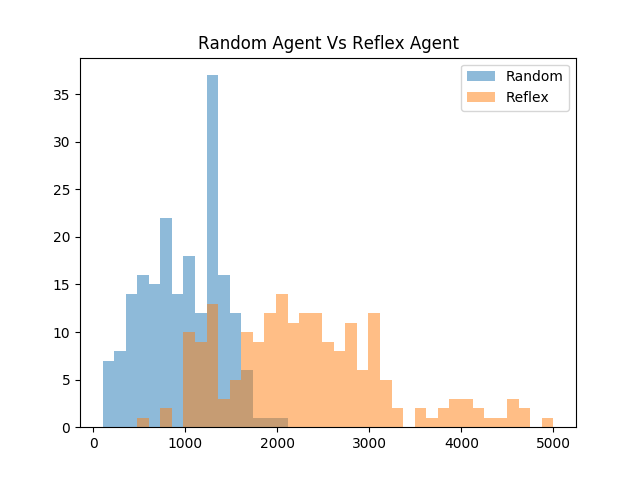
+In this trial, 200 tests of both the random agent and the reflex agent
+were observed while setting the seed of the environment to the current
+time. The seed was randomly set in this scenario since the reflex
+agent is fully deterministic and would perform identically in each trial
+otherwise. 
+
+![histogram](media/asteroids/reflexPerformance.png)
+
+
+The histogram depicts that the reflex agent on average performs
+significantly better than the random agent. What is fascinating to
+note is that even though the agent's actions are deterministic, the
+seed of the environment created a large amount of variance in the
+scores observed. It is arguably misleading to only provide a single
+score for an agent as its performance because the environment seed has
+a large impact on the non-random agent's scores.
+
+```
+Reflex Agent: 
+    mean:2385.25
+    max:8110.0 
+    min:530.0 
+    sd:1066.217115553863 
+    median:2250.0 
+    n:200
+
+Random Agent:
+    mean:976.15 
+    max:2030.0
+    min:110.0 
+    sd:425.2712987023695 
+    median:980.0 
+    n:200
+```
+
+One thing that is interesting about comparing the two distributions is
+that the reflex agent has a much larger standard deviation in its
+scores than the random agent. It is also interesting to note that the
+reflex agent's worst performance was significantly better than the
+random agent's worst performance. Also, the best performance of the
+reflex agent shatters the best performance of the random agent. 
+
+```
+Random agent vs reflex
+F_onewayResult(
+    statistic=299.86689786081956, 
+    pvalue=1.777062051091977e-50
+)
+```
+
+Since we took such a sample size of two hundred, and the populations
+were significantly different, we got a p score of nearly zero
+(1.77e-50). With a p-value like this, we can say with nearly 100%
+confidence (with rounding) that these two populations are different
+and that the reflex agent out-performs the random agent. 
+
+
+
+# Genetic Algorithm
+
+Genetic algorithms employ the same tactics used in natural selection
+to find an optimal solution to an optimization problem. Genetic
+algorithms are often used in high dimensional problems where the
+optimal solutions are not apparent. Genetic algorithms are commonly
+used to tune the hyper-parameters of a program. However, this
+algorithm can be used in any scenario where you have a function that
+defines how well a solution is. 
+
+In the scenario of asteroids, we can employ genetic algorithms to find
+the optimal sequence of moves to make to achieve the highest score
+possible. The chromosomes are well defined as the sequence of actions
+to loop through and the fitness function is simply the score that the
+agent achieves. 
+
+## Algorithm Implementation
+
+The actual implementation of the genetic algorithm was pretty straight
+forward, the agent simply looped through a sequence of events where
+each event represents a gene on the chromosome. 
+
+
+```python
+class Agent(object):
+    """Very Basic GA Agent"""
+    def __init__(self, action_space, chromosome):
+        self.action_space = action_space
+        self.chromosome = chromosome
+        self.index = 0
+
+    # You should modify this function
+    def act(self, observation, reward, done):
+        if self.index >= len(self.chromosome)-1:
+            self.index = 0
+        else:
+            self.index = self.index + 1
+        return self.chromosome[self.index]
+```
+
+
+Rather than using a library, a simple home-brewed genetic algorithm
+was created from scratch. The basic algorithm essentially is in a loop
+that runs functions necessary to iterate through each generation.
+Each generation can be broken apart into a few steps: 
+
+- selection: removes the worst-performing chromosomes
+- mating: uses crossover to create new chromosomes
+- mutation: adds randomness to the chromosome
+- fitness: evaluates the performance of each chromosome
+
+In roughly 100 lines of python, a basic genetic algorithm was crafted.
+
+```python
+AVAILABLE_COMMANDS = [0,1,2,3,4]
+
+
+def generateRandomChromosome(chromosomeLength):
+    chrom = []
+    for i in range(0, chromosomeLength):
+        chrom.append(choice(AVAILABLE_COMMANDS))
+    return chrom
+
+
+"""
+creates a random population
+"""
+def createPopulation(populationSize, chromosomeLength):
+    pop = []
+    for i in range(0, populationSize):
+        pop.append((0,generateRandomChromosome(chromosomeLength)))
+    return pop
+
+
+"""
+computes fitness of population and sorts the array based
+on fitness
+"""
+def computeFitness(population):
+    for i in range(0, len(population)):
+        population[i] = (calculatePerformance(population[i][1]), population[i][1])
+    population.sort(key=lambda tup: tup[0], reverse=True) # sorts population in place
+
+
+"""
+kills the weakest portion of the population
+"""
+def selection(population, keep):
+    origSize = len(population)
+    for i in range(keep, origSize):
+        population.remove(population[keep])
+
+
+
+"""
+Uses crossover to mate two chromosomes together.
+"""
+def mateBois(chrom1, chrom2):
+    pivotPoint = randrange(len(chrom1))
+    bb = []
+    for i in range(0, pivotPoint):
+        bb.append(chrom1[i])
+    for i in range(pivotPoint, len(chrom2)):
+        bb.append(chrom1[i])
+    return (0, bb)
+    
+
+
+"""
+brings population back up to desired size of population
+using crossover mating
+"""
+def mating(population, populationSize):
+    newBlood = populationSize - len(population)
+
+    newbies = []
+    for i in range(0, newBlood):
+        newbies.append(mateBois(choice(population)[1], 
+                                choice(population)[1]))
+    population.extend(newbies)
+
+
+"""
+Randomly mutates x chromosomes -- excluding best chromosome
+"""
+def mutation(population, mutationRate):
+    changes = random() * mutationRate * len(population) * len(population[0][1])
+    for i in range(0, int(changes)):
+        ind = randrange(len(population) -1) + 1
+        chrom = randrange(len(population[0][1]))
+        population[ind][1][chrom] =  choice(AVAILABLE_COMMANDS)
+
+
+"""
+Computes average score of population
+"""
+def computeAverageScore(population):
+    total = 0.0
+    for c in population:
+        total = total + c[0]
+    return total/len(population)
+
+
+def runGeneration(population, populationSize, keep, mutationRate):
+    selection(population, keep)
+    mating(population, populationSize)
+    mutation(population, mutationRate)
+    computeFitness(population)
+
+
+"""
+Runs the genetic algorithm
+"""
+def runGeneticAlgorithm(populationSize, maxGenerations, 
+                        chromosomeLength, keep, mutationRate):
+    population = createPopulation(populationSize, chromosomeLength)
+
+    best = []
+    average = []
+    generations = range(1, maxGenerations + 1)
+
+    for i in range(1, maxGenerations + 1):
+        print("Generation: " + str(i))
+        runGeneration(population, populationSize, keep, mutationRate)
+
+        a = computeAverageScore(population)
+        average.append(a)
+        best.append(population[0][0])
+
+        print("Best Score: " + str(population[0][0]))
+        print("Average Score: " + str(a))
+        print("Best chromosome: " + str(population[0][1]))
+        print()
+
+    pyplot.plot(generations, best, color='g', label='Best')
+    pyplot.plot(generations, average, color='orange', label='Average')
+
+    pyplot.xlabel("Generations")
+    pyplot.ylabel("Score")
+    pyplot.title("Training GA Algorithm")
+    pyplot.legend()
+    pyplot.show()
+```
+
+
+## Results
+
+![training](media/asteroids/GA50.png)
+
+
+![training](media/asteroids/GA200.png)
+
+
+```
+Generation: 200
+Best Score: 8090.0
+Average Score: 2492.6666666666665
+Best chromosome: [1, 4, 1, 4, 4, 1, 0, 4, 2, 4, 1, 3, 2, 0, 2, 0, 0, 1, 3, 0, 1, 0, 4, 0, 1, 4, 1, 2, 0, 1, 3, 1, 3, 1, 3, 1, 0, 4, 4, 1, 3, 4, 1, 1, 2, 0, 4, 3, 3, 0]
+```
+
+It is impressive that a simple genetic algorithm can learn how
+to perform well when the seed is fixed. When compared to the
+random agent which had a max score of 3320 with a fixed seed, the
+optimized genetic algorithm shattered the random agents' best
+performance by a factor of 2.5. 
+
+Since we trained an optimized set of actions to take to achieve a high
+score on a specific seed, what would happen if we randomized the seed?
+A test was conducted to compare the trained GA agent with 200
+generations against the random agent. For both agents, the seed was
+randomized by setting it to the current time.
+
+![200 Trials GA Random Seed](media/asteroids/GAvsRandom.png)
+
+
+```
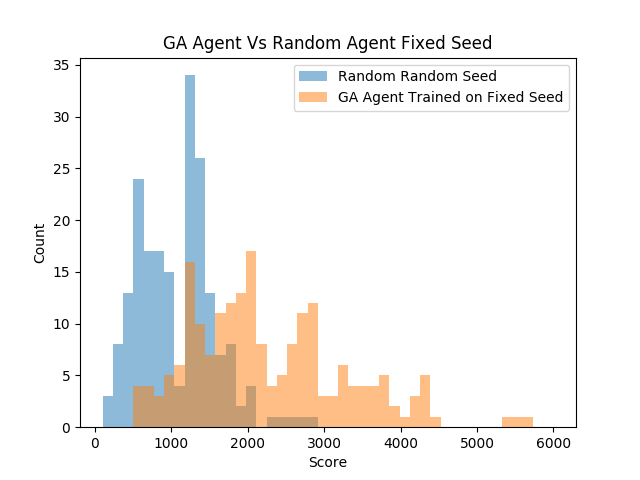
+GA Performance Trained on Fixed Seed:
+    mean:2257.9 
+    max:5600.0
+    min:530.0 
+    sd:1018.4363455808125 
+    median:2020.0 
+    n:200
+```
+
+
+```
+Random Random Seed:
+    mean:1079.45 
+    max:2800.0 
+    min:110.0 
+    sd:498.9340612746338 
+    median:1080.0 
+    n:200
+```
+
+```
+F_onewayResult(
+    statistic=214.87432376234608, 
+    pvalue=3.289638100969386e-39
+)
+```
+
+As expected, the GA agent did not perform as well on random seeds as
+it did on the fixed seed that it was trained on. However, the GA was
+able to find an action sequence that statistically beat the random
+agent as observed in the score distributions above and the extremely
+small p-value. Although luck was a part of getting the agent to get a
+score of 8k on the seed of zero, the skill that it learned was
+somewhat applicable to other seeds. After replaying the video of the
+agent play, it just slowly drifts around the screen and shoots at
+asteroids in front of it. This has a major advantage over the random
+agent since the random agent tends to move very fast and rotate
+spastically. 
+
+## Future Work
+
+This algorithm was more or less a last-minute hack to see if I can
+make a cool video of a high scoring asteroids agent. Future agents
+using genetic algorithms would incorporate reflex to dynamically
+respond to the environment. Based on which direction asteroids are in
+proximity to the player, the agent could select a different chromosome
+of actions to execute. This would potentially yield scores above ten thousand if trained and implemented correctly. Future training
+should also incorporate randomness to the seed so that the skills
+learned are the most transferable to other random environments. 
+
+# Deep Q-Learning Agent
+
+## Introduction:
+
+
+The inspiration behind attempting a reinforcement learning agent for
+this problem scope is the original DQN paper that came out from
+Deepmind, “Playing Atari with Deep Reinforcement Learning.” This paper
+showed the potential of utilizing this Deep Q-learning methodology on
+a variety of simulated Atari games using one standardized architecture
+across all. Reinforcement learning has always been of interest and to
+have the opportunity to spend time learning about it while applying
+for a class setting was exciting, even if it is out of the scope of
+the class presently. It has been an exciting challenge to read through
+and implement a research paper to get similar results. 
+
+Deep Q-Learning is an extension of the standard Q-Learning algorithm
+in which a neural network is used to approximate the optimal
+action-value function, Q\*(s,a). The action-value function is the
+function that outputs the expected maximum reward given a state and a
+policy mapping to actions or distributions of actions. Logically, this
+works as the Q function follows the Bellman equation identity, which
+states that if the optimal action for the next step state is known,
+then the optimal output given an action a’ follows by maximizing the
+expected reward of the equation, r+Q*(s',a'). Thus, the reinforcement
+learning part comes in the form of a neural network approximating the
+optimal action-value function by using the Bellman equation identity
+as an iterative update at every time step. 
+
+
+## Agent architecture: 
+
+The basis of the network architecture is a basic convolutional network
+with 2 conv layers, a fully connected layer, and then an output layer
+of 14 classes with each representing an individual action. The first
+layer consists of 16 8x8 filters and takes a stride 4 while the second
+has 32 4x4 filters and only takes a stride of 2. Following this layer,
+the filters are compressed into a 1-D representation vector of size
+12,672 that’s passed through a fully connected layer of 256 nodes. 
+
+All layers sans the output layer are activated using the ReLU function.
+The optimization algorithm of choice was the Adam optimizer, using a
+learning rate equal to .0001 and default betas of [.9, .99]. The
+discount factor, or gamma, related to future expected rewards was set
+at .99 and the probability of taking a random action per action step
+was linearly annealed from 1.0 down to a fixed .1 after one million
+seen frames. 
+
+![Layer code](media/asteroids/code.png)
+
+
+## Experience Replay:
+
+One of the main points within the original paper that significantly
+helped the training of this network is the introduction of a Replay
+Buffer that is used during the training. To break all the
+temporal correlation between sequential frames and biasing the
+training of a network-based off certain chains of situations, a
+historical buffer of transitions is used to sample mini-batches to
+train on per time step. Every time an action is made, a tuple
+consisting of the current state, the action is taken, the reward gained, and
+the subsequent state (s, a, r, s’) is stored into the buffer. And at
+every training step, a mini-batch is sampled from the buffer and used
+to train the network. This allows the network to be trained in
+non-correlated transitions and hopefully train in a more generalized
+way to the environment rather than biased to a string of similar
+actions. 
+
+## Preprocessing:
+
+One of the first issues that had to be tackled was the issue of the
+high dimensionality of the input image and how that information was
+duplicated stored in the Replay Buffer. Each observation given from
+the environment is a matrix of (210, 160, 3) pixels representing the
+RGB pixels within the frame. For time and being
+computationally efficient, it was needed to preprocess and reduce the
+dimensionality of the observations as a single frame stack (of which
+there are two per transition) consists of (4, 3, 210, 160) or 403,000
+input features that would have to be dealt with. 
+
+![Before Processing](media/asteroids/dqn_before.png)
+
+Firstly, images are converted into a grayscale image and the
+reward/number lives section at the top of the screen is cut out since
+it is irrelevant to the network’s vision. Furthermore, the now (4,
+192, 160) matrix was downsampled by taking every other pixel to (4,
+96, 80), resulting in a change from 403,000 input features to only
+30,720 - a substantial reduction in the calculations needed while
+maintaining strong input information for the network. 
+
+![After Processing](media/asteroids/dqn_after.png)
+
+
+## Training:
+
+Training for the bot was conducted by modifying the main function to
+allow games to immediately start after one was finished, to
+make continuous training of the agent easier. All the environment
+parameters were reset and the temporary attributes of the agent (ie.
+current state/next state) were flushed. For the first four frames of a
+game, the bot just gathered a stack of frames. And following that, at
+every time the next state was compiled and the transition tuple pushed
+onto the buffer, as well as a training step for the agent. For the
+training step, a random batch was grabbed from the replay buffer and
+used to calculate the loss function between actual and expected
+Q-values. This was used to calculate the gradients for the
+backpropagation of the network. 
+
+
+## Outcome:
+
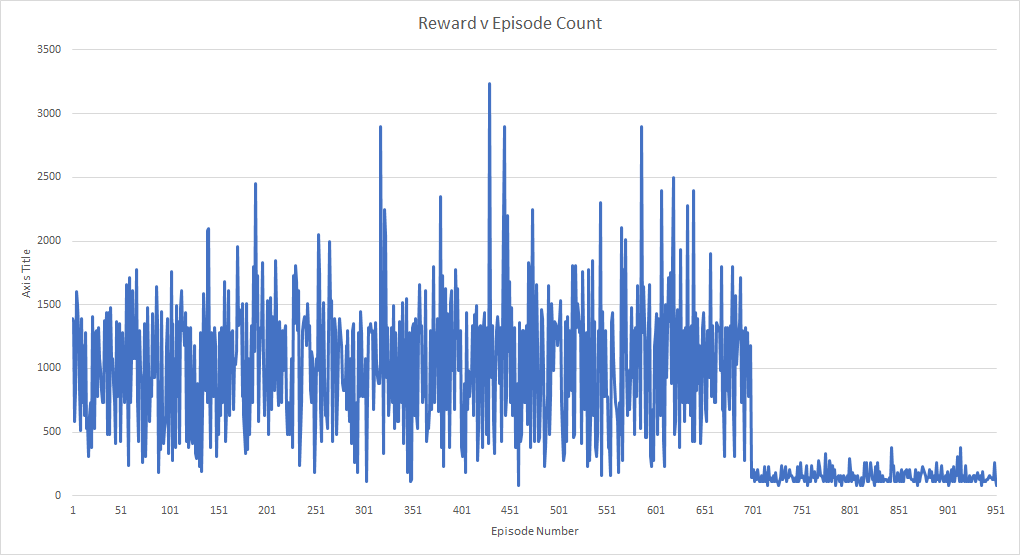
+Unfortunately, the result of 48 hours of continuous training, 950
+games played, and roughly 1.3 million frames of game footage seen, was
+that the agent converged to a suicidal policy that resulted in a
+consistent garbage performance. 
+
+![Reward](media/asteroids/reward.png)
+
+
+The model transitioned to the fixed 90% model action chance around
+episode 700, which is exactly where the agent starts to go awry. The
+strange part about this is since the random action chance is linearly
+annealed over the first million frames, if the agent had continuously
+been following a garbage policy, it would’ve been expected that the
+rewards would steadily decrease over time as the network takes more
+control.
+
+![Real Trendline](media/asteroids/reward_trendline.png)
+
+
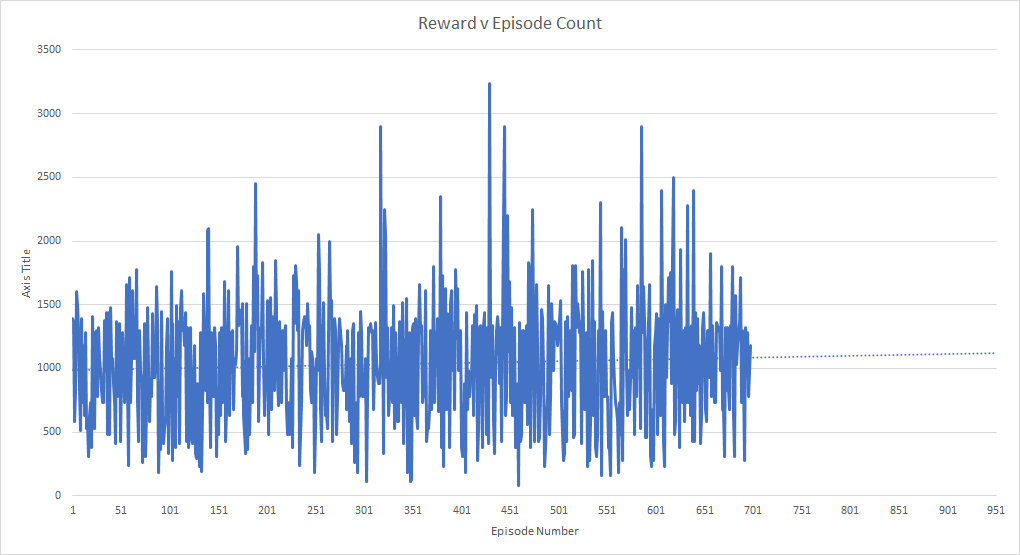
+Up until that point, the projection of the reward trendline was a
+steady rise per the number of episodes. Expanding this out until
+10,000 frames (approximately 10 million frames seen, the same amount
+of time the original Deepmind paper trained these bots for), the
+projected score is in the realms of 2,400 to 2,500 - which matches up
+closely to the well-tuned reflex agent and the GA agent on a random
+seed. 
+
+![Endgame Trendline](media/asteroids/reward_projection.png)
+
+
+It would’ve been exciting to see how the model compared to
+our reflex agent had it been able to train consistently up until the
+end. 
+
+## Limitations:
+
+There were a fair number of limitations that were present within the
+execution and training of this model that possibly contributed to the
+slow and unstable training of the network. Differences in the
+algorithm from the original paper is that the optimization function
+utilized was the Adam optimizer instead of RMSProp and the replay
+buffer only took into consideration the previous 50k frames, not the
+past one million. It might be possible that the weaker replay buffer
+was to blame as the model was continuously fed a sub-optimal within
+its past 50,000 frames that caused it to diverge so heavily near the
+end. 
+
+One issue in preprocessing that might've led the bot astray is using
+not using the max pixelwise combination between sequential frames in
+order to have each frame include both the asteroids and the player.
+Since the Atari (and by extension, this environment simulation)
+doesn't render the asteroids and the player sprite all in the same
+frame, it is possible that the network was unable to extract any
+coherent connection between the alternating frames. 
+
+Regarding optimizations built on the DQN algorithm past the original
+Deepmind paper, we did not use a policy and a target network in
+training. In the original algorithm, the estimation and attempt at
+converging to the target policy is unstable due to the target
+network’s weights continuously shifting during training. For the
+network, it’s hard to converge to something that’s continually
+shifting at every time step and leads to very noisy and unstable
+training. One optimization that has been proposed for DQN is to have a
+policy and target network. At every timestep, the policy network’s
+weights are updated with the calculated gradients while the target
+network is maintained for a number of steps. This lets the target
+policy be still for a few time steps while the network is converging
+to it and leads to more stable and guided training. 
+
+Perhaps the largest limitation in training was the computational power
+used for training. The network was trained on a single GTX1060ti GPU,
+which led to just single episodes taking a few minutes to complete. It
+would’ve taken an incredibly long time to hit 10 million seen frames
+as even just 1.3 million took approximately 48 hours. It’s probable
+that our implementation is inefficient in its calculations, however it
+is a well known limitation of RL that it is time and computationally
+intensive. 
+
+## Deep Q Conclusions:
+
+This was a fun agent and algorithm to implement, even if at present it
+has given little to no results back in terms of performance. The plan
+is to continue testing and training the agent, even after the
+deadline. Reinforcement learning is a complicated and hard to debug
+environment, but similarly an exciting challenge due to its potential
+for solving and overcoming problems. 
+
+
+# Conclusion
+
+This project demonstrated how fun it can be to train AI agents to play
+video games. Although none of our agents are earth-shatteringly
+amazing, we were able to use statistical measures to determine that
+the reflex and GA agents outperformed the random agent. The GA agent
+and the convolutional neural network show very promising and future
+work can be used to drastically improve their results.