8 changed files with 96 additions and 0 deletions
+ 96
- 0
blogContent/posts/data-science/datafest-2019.md
View File
BIN
blogContent/posts/data-science/media/datafest/clusterMess.png
View File
BIN
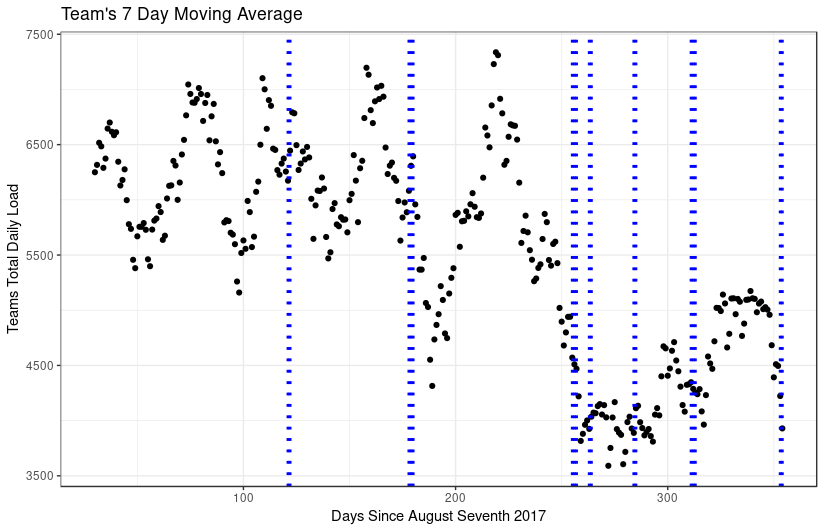
blogContent/posts/data-science/media/datafest/hoursOfSleepBoxPlot.png
View File
BIN
blogContent/posts/data-science/media/datafest/hoursOfSleepDensity.png
View File
BIN
blogContent/posts/data-science/media/datafest/network.png
View File
BIN
blogContent/posts/data-science/media/datafest/noShit.png
View File
BIN
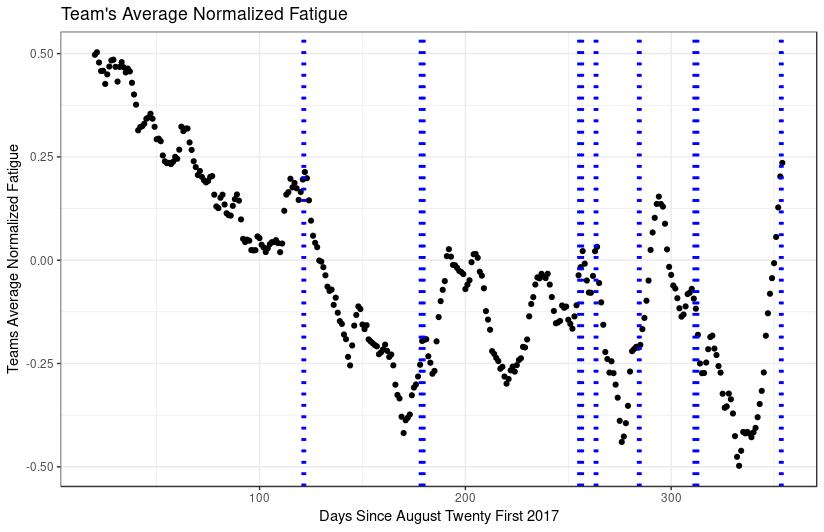
blogContent/posts/data-science/media/datafest/teamFatigue.png
View File
BIN
blogContent/posts/data-science/media/datafest/teamWork.png
View File
Loading…