Initial outline of datafest blog post.

blogContent/posts/data-science/datafest-2019.md

@@ -0,0 +1,96 @@
+
+
+# Importing and Cleaning Data
+
+
+# Data Visualization
+
+
+# Analysis
+
+
+# Report
+
+
+
+## Abstract
+
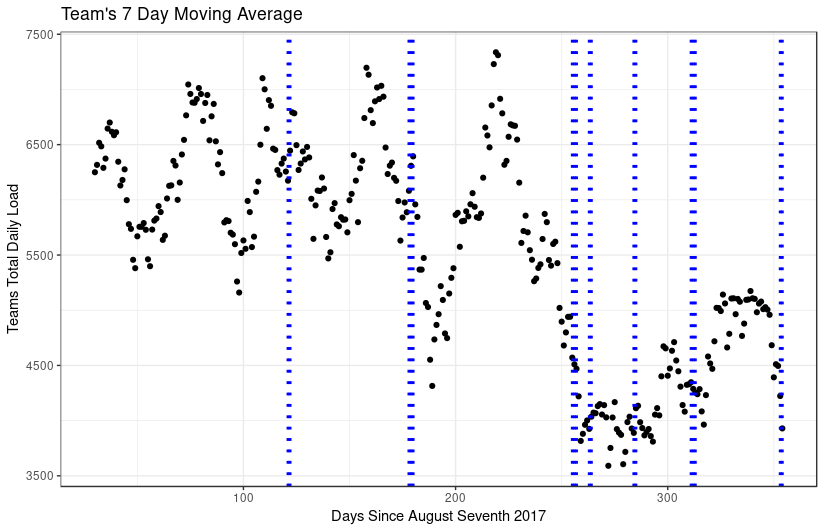
+The way in which a team trains is critical in ensuring that everyone performs at their peak performance
+during a game. In order to effectively train a team to optimize their gameday performance, it would make
+intuitive sense to monitor their training data with respect to their perceived fatigue. Through analyzing
+time series data provided by our partnering women’s rugby team, it was observed that this team altered
+their training schedule close to games. Although there is some relationship between the two in the long
+run, our attempts at modeling fatigue and work load in the short run suggests little to no correlation using
+linear regressions. This suggests that modeling fatigue is a more complex problem including a slew of factors
+both psychological and physical which spans over a period of time; coaches should pay attention not only to
+training but also sleep and mental wellness for happy and competitive teams. To most effectively forecast an
+individual’s performance during a game, we propose a system which takes into account physiological factors
+such as desire and physical factors such as sleep, soreness and amount of training.
+
+## Methodology
+
+We employed a wide range of techniques for establishing our models and hypotheses, including smoothing
+of time series Information, testing of hypotheses based on a prior understanding of the domain, plotting
+and visually analyzing pairs of variables, and artificial intelligence algorithms that found various linear and
+nonlinear patterns in the dataset. Coefficients of determination were calculated to determine fitness of linear
+models, and F1 scores were analyzed to validate complex nonlinear classification models.
+
+
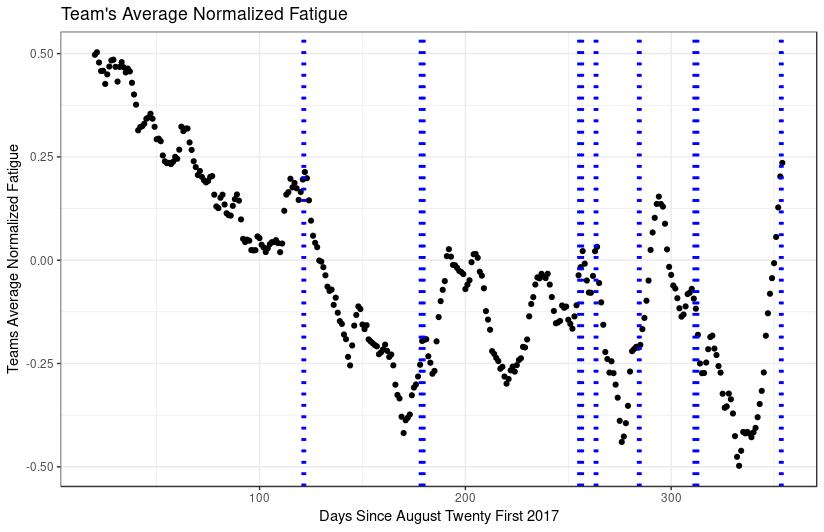
+## Modeling Fatigue
+
+Fatigue can be effectively and linearly modeled using daily records and time series moving
+averages of acute chronic ratios, daily workload, sleep quality, and sleep hours.
+This means that instead of only lowering training before competitions, coaches
+should put focus on preparing the athletes physically and mentally through a
+combination of measures with a focus on sleep.
+
+
+| Iterations/100      | Mean Squared Error |
+| ----------- | ----------- |
+| 1      | 90.4998       |
+| 11   | 1.0265        |
+| 21   | 0.9604        |
+| 31   | 0.8671        |
+| 41   | 0.7838        |
+|100 | 0.0925 |
+Sample Size: 304864
+Final R2: 0.532
+
+
+## Predicting Performance
+
+Trivially, performance of an individual cannot be modeled using simple linear regressions 
+only involving one factors. We therefore developed and optimized a deep neural
+ network to capture the patterns involving fatigue, sleep, and self-rated performance. 
+
+The structure of the network is a 3-layer (input, output, and a hidden layer) 
+sigmoid classifier that was trained on batches of 32 samples from players with 
+respect to features: normalized perceived fatigue, sliding average of
+perceived fatigue, sliding average over sleep hours, and the perceived sleep quality of
+the players. It is optimized through the Adam optimizer with a learning rate of 
+.005 and cross entropy to calculate the loss between the logits and labels. 
+   
+The logits of the work are a confidence output on which class the network
+feels the sample most likely belongs to, the real value of which is the 
+classification of perceived performance by the player. Through this method,
+we can show a correlation between fatigue, sleep, and self-rated performance,
+as well as a means to predict this self-rate performance based off of fatigue
+and self-perceived sleep quality.
+
+Results with LR=.01, Batch=32:
+
+- Accuracy before training: 20.44388%
+- Loss after step 49: .531657
+- Accuracy after training: 74.846625%
+- F1 Score: .94
+
+![](media/datafest/network.png)
+
+## Future Work
+
+With more data to to test with we can further improve and validate out models. With historical data from
+other teams we can take our analysis one step further. Based on the training, performance, and fatigue
+information from other teams we can use that to create a model to make a recommendation for our team’s
+training. This model would be able to make recommendations for our training intensity leading up to a
+game. Since this will be heavily dealing with multivariate time series data leading up to a game, using a Long
+Short-term Network (LSTM) would bring promising results.