15 KiB
| layout | title |
|---|---|
| post | PageRank |
In this section, we study PageRank which is a method for ranking webpages by importance using link structure in the web graph. This is a commonly used algorithm for web search popularized by Google. Before discussing PageRank, let us first conceptualize the web as a graph and attempt to study its structure using the language of graph theory.
The web as a graph
We can represent the entire web as a graph by letting the web pages be nodes and the hyperlinks connecting them be directed edges. We will also make a set of simplifying assumptions:
- Consider only static webpages
- Ignore dark matter on the web (i.e. inaccessible material, pages behind firewalls)
- All links are navigable. Transactional links (eg: like, buy, follow etc.) are not considered
Conceptualizing the web this way is similar to how some popular search engines view it. For instance, Google indexes web pages using crawlers that explore the web by following links in a breadth-first order. Some other examples of graphs that can be viewed this way are: the graph of citations between scientific research papers, references in an encyclopedia.
What does the graph of the web look like
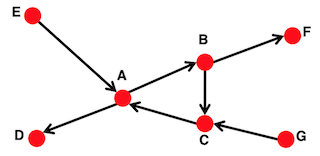
In the year 2000, the founders of AltaVista ran an experiment to explore what the Web looked like. They asked the question: given a node $$v$$: what are the nodes $$v$$ can reach? What other nodes can reach $$v$$?
This produced two sets of nodes:
$$
In(v) = { w| w \textrm{ can reach } v}\
Out(v) ={ w| v \textrm{ can reach } w}
$$
These sets can be ascertained by running a simple BFS. For example, in the following graph:
$$
In(A) = {A,B,C,E,G}\
Out(A) = {A,B,C,D,F}
$$
More on directed graphs
There are two types of directed graphs:
- Strongly connected graphs: A graph where any node can reach any other node.
- Directed Acyclic Graph (DAG): A graph where there are no cycles and if $$u$$ can reach $$v$$, then $$v$$ cannot reach $$u$$
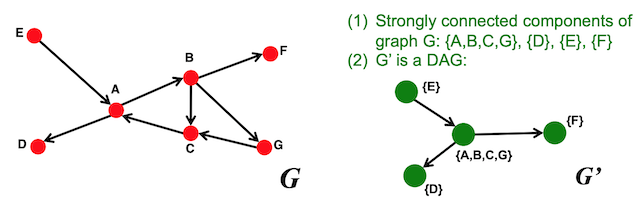
Any directed graph can be represented as a combination of these two types. To do so:
- Identify the strongly connected components (SCCs) within a directed graph: An SCC is a set of nodes $$\textbf{S}$$ in a graph $$\textbf{G}$$ that is strongly connected and that there is no larger set in $$\textbf{G}$$ containing $$\textbf{S}$$ which is also strongly connected. SCCs can be identified by running a BFS on all in-links into a given node and another BFS on all the out-links from the same node and then calculating the intersection over these two sets.
- Merge the SCCs into supernodes, creating a new graph G': Create an edge between the nodes of G' if there is an edge between corresponding SCCs in G. G' is now a DAG
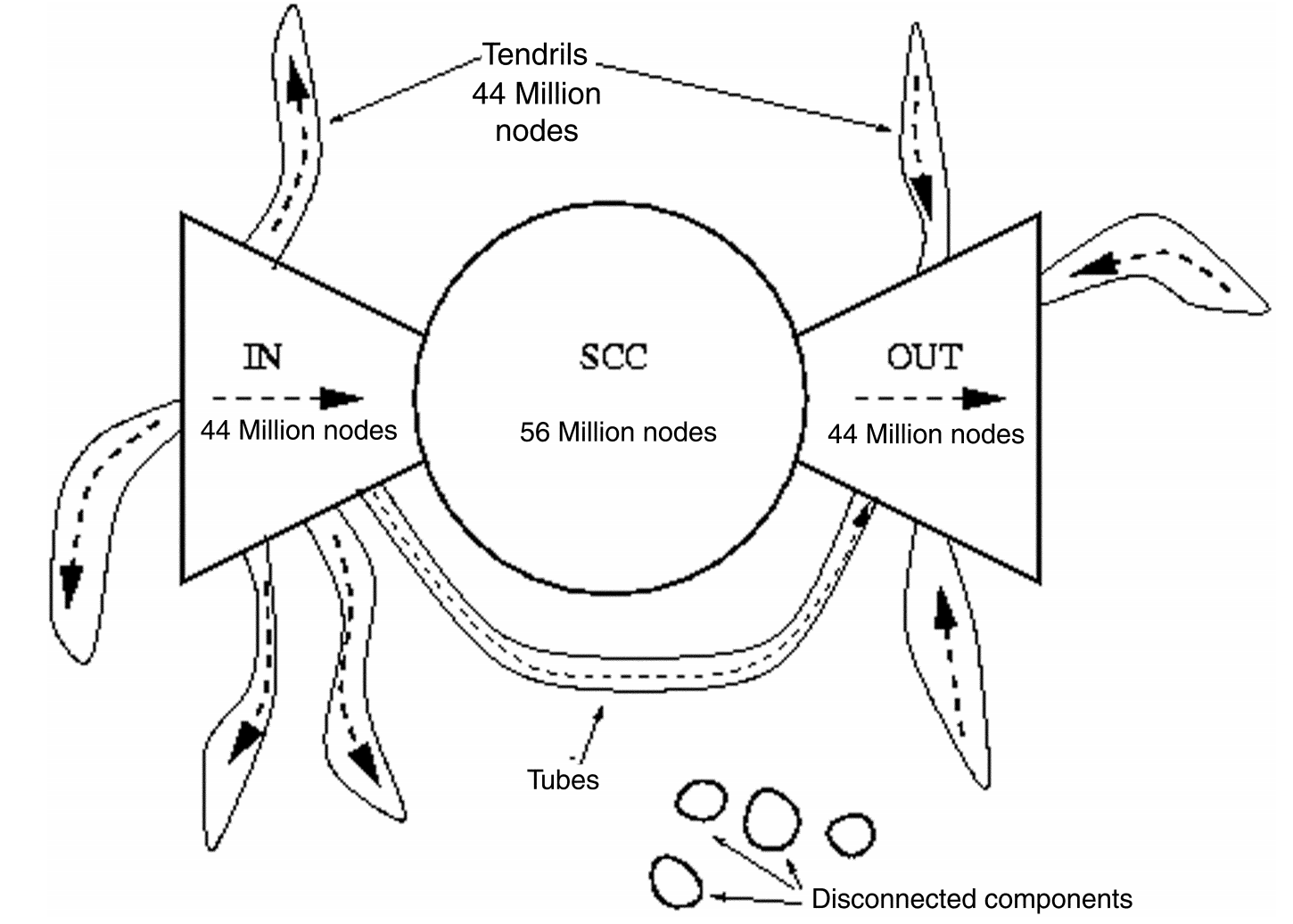
Bowtie structure of the web graph
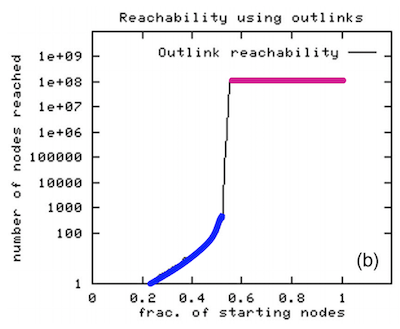
Broder et al. (1999) took a large snapshot of the web and tried to understand how the SCCs in the web graph fit together as a DAG
- Their findings are presented in the figure below. Here the starting nodes are sorted by the number of nodes that BFS visits when starting from that node
- If you look at the nodes on the left colored blue, they are able to reach a very small number of nodes before stopping
- If you look at the nodes on the right colored magenta, they are able to reach a very large number of nodes before stopping
- Using this, we can determine the number of nodes in the IN and OUT component of the bowtie shaped web graph shown below.
- SCC corresponds to the largest strongly connected component in the graph.
- The IN component corresponds to nodes which have out-links to SCC but no in-links from SCC. The OUT component corresponds to nodes which have in-links from SCC but no out-links to SCC.
- Nodes with both in and out links to the SCC fall in SCC.
- Tendrils correspond to edges going out from IN, or to edges going into OUT. TUBES are connections from IN to OUT that bypass SCC.
- Disconnected components are not connected to SCC at all
PageRank - Ranking nodes on the graph
Not all pages on the web are equal. When we run a query, we don’t want to find all the pages that contain query words. Instead, we want to learn how we rank the pages. How can we decide on the importance of pages based on the link structure of the web graph?
The main idea here is that links are votes
In-links into a page are counted as votes for that page which helps determine the importance of the page. In-links from important pages count more. This turns into a recursive relationship: page A's importance depends on page B, whose importance depends on page C and so on.
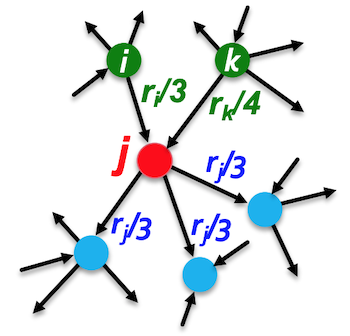
Each link's vote is proportional to the importance of its source page. In the figure below, node $$j$$ has links from $$i$$ and $$k$$ which each contribute importance values equal to $$\frac{r_i}{3}$$ and $$\frac{r_k}{4}$$. This is because there are three out-links from node $$i$$ and four out-links from node $$k$$. Similarly, node $$j$$'s importance is equally distributed between the three out-links that it shares with other nodes.
To summarize, a page is important if it is pointed to by other important pages. Given a set of pages, we can define the page rank $$r_j$$ for node $$j$$ as:
$$ \textbf{r}j = \sum{i\rightarrow j}\frac{\textbf{r}_i}{d_i} $$
where $$i$$ refers to every node that has an outgoing edge into $$j$$ and $$d_i$$ is the out degree of node i.
Matrix formulation
We can formulate these relationships as $$N$$ PageRank equations using $$N$$ variables. We could use Gaussian elimination to solve but this would take a very long time for large graphs such as the web graph.
Instead, we can represent the graph as an adjacency matrix $$\textbf{M}$$ that is column stochastic. This means that all the columns must add up to 1. So for node $$j$$ all the entries, in column $$j$$ will sum to 1.
$$
\textrm{If } j \rightarrow i \textrm{ , then } \textbf{M}_{ij} = \frac{1}{d_j}\
$$
$$r_i$$ is the importance score of page $$i$$
$$ \sum_i \textbf{r}_i = 1 $$
This will fulfill the requirement that the importance of every node must sum to 1. We now rewrite the PageRank vector as the following matrix equation:
$$ \textbf{r} = \textbf{M}.\textbf{r} $$
In this case, the PageRank vector will be the eigenvector of the stochastic web matrix $$\textbf{M}$$ that corresponds to the eigenvalue of 1.
Random walk formulation
PageRank relations are very related to random walks. Imagine a web graph and a random surfer that surfs the graph. At any time $$t$$, the surfer is at any page $$i$$. The surfer will then select any outgoing link uniformly at random and make a new step at time $$t+1$$, and this process continues infinitely. Let $$p(t)$$ be the vector whose $$i$$th component is the probability that a surfer is at page $$i$$ at time $$t$$. $$p(t)$$ is then a probability distribution over pages at a given time $$t$$.
$$ p(t+1) = \textbf{M}\cdot p(t) $$
As $$t$$ approaches infinity, the random walk will reach a steady state:
$$ p(t+1) = \textbf{M}\cdot p(t) = p(t) $$
When we solve the equation $$\textbf{r}=\textbf{M}\cdot \textbf{r}$$; $$\textbf{r}$$ is really just the probability distribution of where this surfer will be at time $$\textbf{t}$$, when $$t$$ approaches infinity. It’s modeling the stationary distribution of this random walker process on the graph.
Power law iteration
Starting from any vector $$u$$, the limit $$\textbf{M}(\textbf{M}(… \textbf{M}(\textbf{M} \textbf{u})))$$ is the long-term distribution of the surfers. In other words, r is the limit when we take a vector $$u$$ and multiply with $$\textbf{M}$$ long enough. This means that we can efficiently solve for $$\textbf{r}$$ using power iterations.
Limiting distribution = principal eigenvector of $$\textbf{M}$$ = PageRank
Initialize: $$ \textbf{r}^{(0)} = [\frac{1}{N},...,\frac{1}{N}]^T$$\
Iterate: $$\textbf{r}^{(t+1)} = \textbf{M}.\textbf{r}^{(t)}$$\
Stop when: $$|\textbf{r}^{(t+1)} - \textbf{r}^{(t)} | < \epsilon $$
We keep iterating until we converge based on epsilon. In practice, this tends to converge within 50-100 iterations.
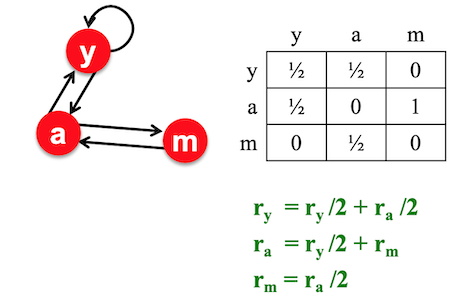
Example
The $$\textbf{r}$$ vector you are left with is the page rank or page importances. So page $$y$$ has importance $$\frac{6}{15}$$, page $$a$$ has importance $$\frac{6}{15}$$ and page $$m$$ has importance $$\frac{3}{15}$$
PageRank: Problems
-
Dead ends: These are pages that have in-links but no out-links. As a random surfer, it’s like coming to a cliff and having nowhere else to go. This would imply that the adjacency matrix is no longer column stochastic and will leak out importance.
-
Spider traps:: These are pages with only self-edges as outgoing edges causing the surfer to get trapped. Eventually the spider trap will absorb all importance. Given a graph with a self-loop in $$b$$, the random surfer will eventually navigate to $$b$$ and get stuck in $$b$$ for the rest of the iterations. Power iteration will converge with $$b$$ having all the importance and leave $$a$$ with no importance.
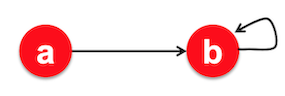
How do we solve this? Using random teleportation or random jumps!
Whenver a random walker makes a step, the surfer has two options. It can flip a coin and with probability 𝜷 continue to follow the links, or with probability $$(1- 𝜷)$$ it will teleport to a different webpage. Where do you jump? to any of the nodes with equal probability. Usually 𝜷 is set around 0.8 to 0.9.
In case of a spider trap: Teleport out in a finite number of steps.\
In case of a dead end: Teleport out with a total probability of 1. This will make the matrix column stochastic.
Putting this together, the PageRank equation (as proposed by Brin-Page, 98) can be written as:
$$ r_j = \sum_{i \rightarrow j} \frac{r_i}{d_i} + (1 - 𝜷) \frac{1}{N} $$
We can now define the Google Matrix A and apply power iteration to solve for $$\textbf{r}$$ as before
$$ A = 𝜷\textbf{M} + (1 - 𝜷)[\frac{1}{N}]_{NXN} $$
$$ \textbf{r} = \textbf{A} \cdot \textbf{r} $$
Note: This formulation assumes that $$\textbf{M}$$ has no dead ends. We can either preprocess matrix $$\textbf{M}$$ to remove all dead ends or explicitly follow random teleport links with probability 1.0 from dead-ends.
Computing PageRank: Sparse matrix formulation
The key step in computing page rank is the matrix-vector multiplication
$$ \textbf{r}{new} = \textbf{A} \cdot \textbf{r}{old} $$
We want to be able to iterate this as many times as possible. If $$\textbf{A}$$, $$\textbf{r}{old}$$, $$\textbf{r}{new}$$ are small and can fit in memory then there is no problem. But if $$N$$ = 1 billion pages and each entry is 4 bytes, then just for storing $$\textbf{r}{old}$$ and $$\textbf{r}{new}$$, we would need 8GB of memory. Matrix A would have $$N^2 = 10^{18}$$ entries, which would require close to 10 million GB of memory!
We can rearrange the computation to look like this:
$$ \textbf{r} = 𝜷 \textbf{M} \cdot \textbf{r} + \frac{[𝟏 − 𝜷]}{𝑵} $$
This is easier to compute because $$\textbf{M}$$ is a sparse matrix, multiplying it with a scalar is still sparse, and then multiplying it with a vector is not as computationally intensive. After this, we simply add a constant which is the probability of the random walker directly jumping to $$\textbf{r}_{new}$$. The amount of memory that we now need goes down from $$O(N^2)$$ to $$O(N)$$. At every iteration, some of the pagerank can leak out and by renormalizing M we can re-insert the leaked page rank.
Here is an example of how PageRank would work if applied it to a graph:
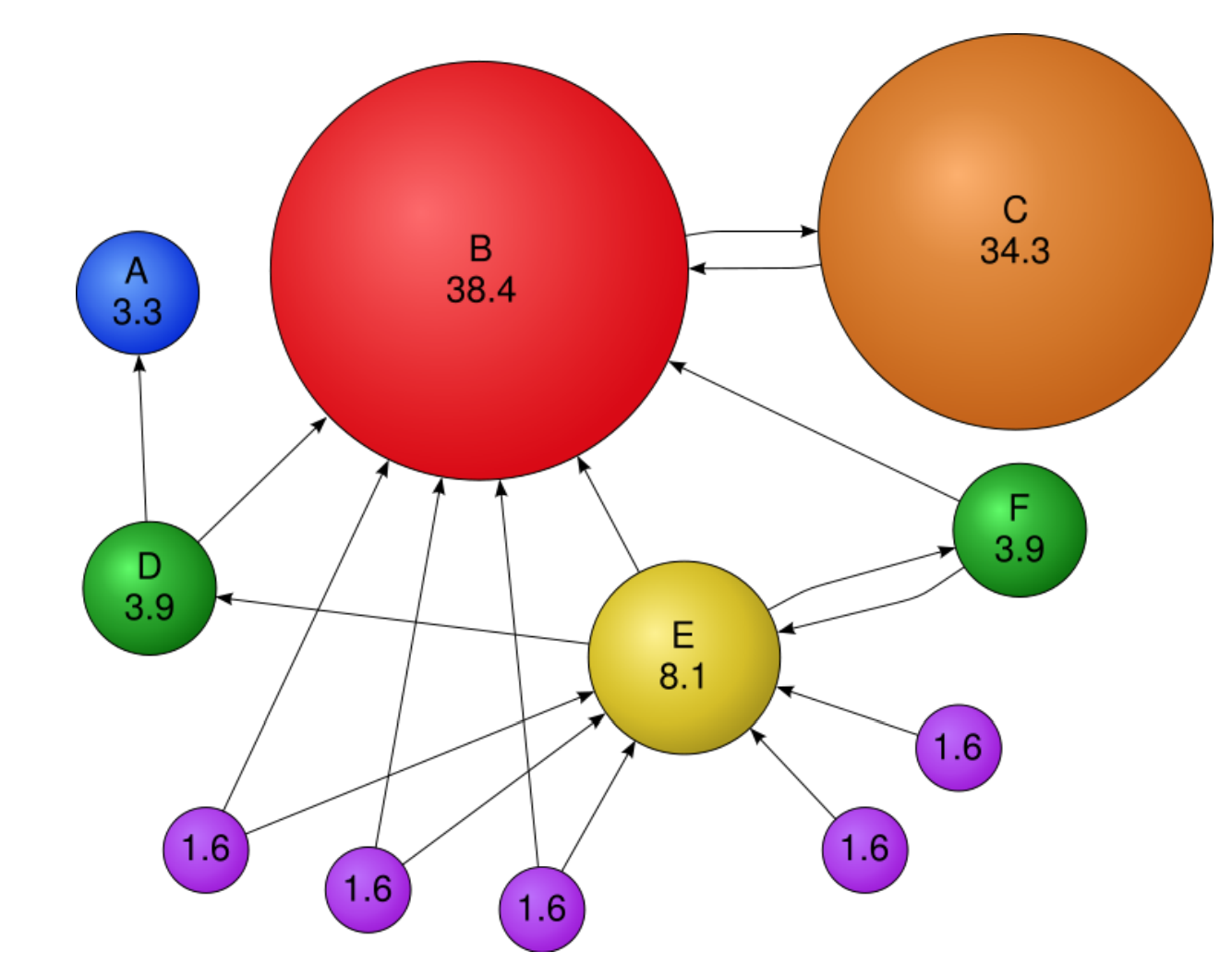
In the figure above, within each node is its pagerank score or importance score. Scores sum to 100, size of the node is proportional to its score. Node B has very high importance because a lot of nodes point to it. These nodes still have importance without in-links because random walker jump can jump to them. Node C has only one-link but since its from B it also becomes very important. However, C's importance is still less than B because B has a lot of other in-links going into it.
PageRank Algorithm
Input:
- Directed graph G (can have spider traps and dead ends)
- Parameter 𝜷
Output:
- PageRank vector $$r^{new}$$
Set: $$r_j^{old} = \frac{1}{N}$$:
Repeat until convergence:
$$ \sum_j|r_j^{new} - r_j^{old}| < \epsilon $$
$$
\forall j: r_j^{'new} = \sum_{i \rightarrow j}𝜷 \frac{r_i^{old}}{d_i}\
r_j^{'new} = 0 \textrm{ if in-degree of j is } 0
$$
Now re-insert the leaked PageRank:
$$
\forall j: r_j^{new} = r_j^{'new} + \frac{1-s}{N} \textrm{ where } S = \sum_jr_j^{'new}\
r^{old} = r^{new}
$$
Personalized PageRank and random walk with restarts
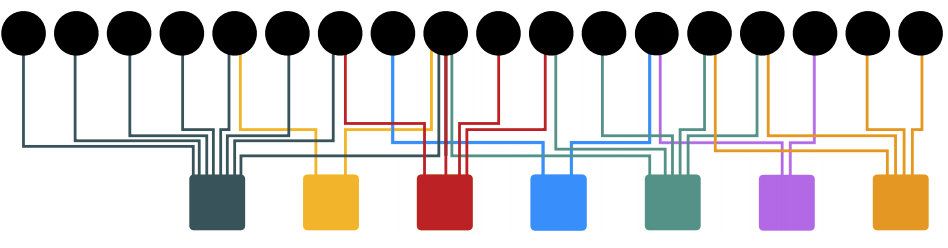
Imagine we have a bipartite graph consisting of users on one side (circles in the figure below) and items on the other (squares). We would like to ask how related two items are or how related two users are. Given that the users have already purchased in the past - what can we recommend to them, based on what they have in common with other users.
We can use different metrics to quantify this such as shortest path or number of common neighbors, however these are not very versatile. Instead, we can use a modified version of PageRank that doesn't rank all pages by importance rather it ranks them by proximity to a given set. This set is called the teleport set $$\textbf{S}$$ and this method is called Personalized PageRank.
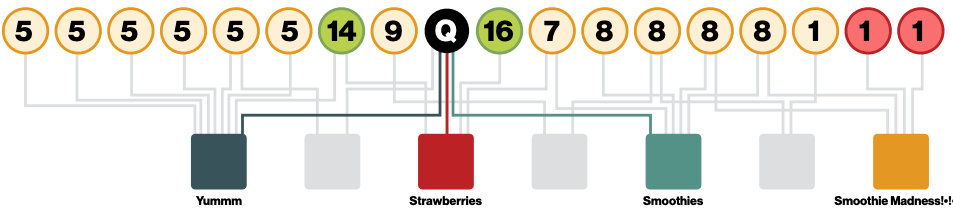
One way to implement this is to take the teleport set and compute the pagerank vector using power iteration. However, in this case, since we only have a single node in S, its quicker to just do a simple random walk. So, the random walker starts at node $$\textbf{Q}$$ and then whenever it teleports it goes back to $$\textbf{Q}$$. This will give us all the nodes that are most similar to $$\textbf{Q}$$ by identifying those with the highest visit counts. We thus achieve a very simple recommender system that works very well in practice, and we can call it random walk with restarts.
Random walk with restarts is able to account for
- Multiple connections
- Multiple paths
- Direct and indirect connections
- Degree of the node
PageRank Summary:
-
Normal pagerank: Teleportation vector is uniform
-
Personalized PageRank: Teleport to a topic specific set of pages. Nodes can have different probabilities of surfer landing there
-
Random walk with restarts: Topic specific pagerank where teleport is always to the same node. In this case, we don't need power iteration we can just use random walk and its very fast and easy