5.8 KiB
| layout | title | header-includes |
|---|---|---|
| post | Network Effects And Cascading Behaviour | [\usepackage{amsmath}] |
The phenomenon of spreading through networks and cascading behaviors is prevalent in a wide range of real networks. Examples include contagion of diseases, cascading failure of technologies, diffusion of fake news, and viral marketing. Formally, an “infection” event can spread contagion through main players (active/infected nodes) which constitute a propagation tree, known as a cascade. We will examine two model classes of diffusion:
- Decision-based: each node decides whether to activate based on its neighbors' decisions. Deterministic rule, nodes are active players, and suited for modeling adoption
- Probabilistic: infected nodes "push" contagion to uninfected nodes with some probability. Can involve randomness, nodes are passive, and suited for modeling epidemic spreading
Decision Based Diffusion
Game Theoretic Model of Cascades: single behavior adoption
The key intuition behind the game theoretic model is that a node will gain more payoff if its neighbors adopt the same behavior as it. An example is competing technological products: if your friends have the same type DVD players and discs (e.g. Blu-ray vs. HD DVD), then you can enjoy sharing DVDs with them.
Every node independently decides whether to adopt the contagion depending upon its neighbors. The decision is modelled as a two-player game between a node and a given neighbor. Hence a node with degree $$k$$ plays $$k$$ such games to evaluate its payoff and correspondingly its behavior. The total payoff is the sum of node payoffs over all games.
If there are two behavior $$A$$ and $$B$$ in the network and each node can adopt a single behavior, the payoff matrix for the two-player game is as follows:
| A | B | |
|---|---|---|
| A | a | 0 |
| B | 0 | b |
where rows correspond to node $$v$$'s behavior, columns correspond to node $$w$$'s behavior, and entries represent each node's payoff.
Let's analyze a node with $$d$$ neighbors, and let $$p$$ be the fraction of nodes which have adopted $$A$$. The payoff for choosing $$A$$ is $$apd$$ and the payoff for choosing $$B$$ is $$b(1-p)d$$. Hence the node adopts behavior $$A$$ if the following is met: $$apd > b(1-p)d \implies p > \frac{b}{a+b}$$
We define $$q = \frac{b}{a+b}$$ to be the threshold fraction of a node's neighbors required for the node to choose $$A$$ i.e. requires $$p > q$$.
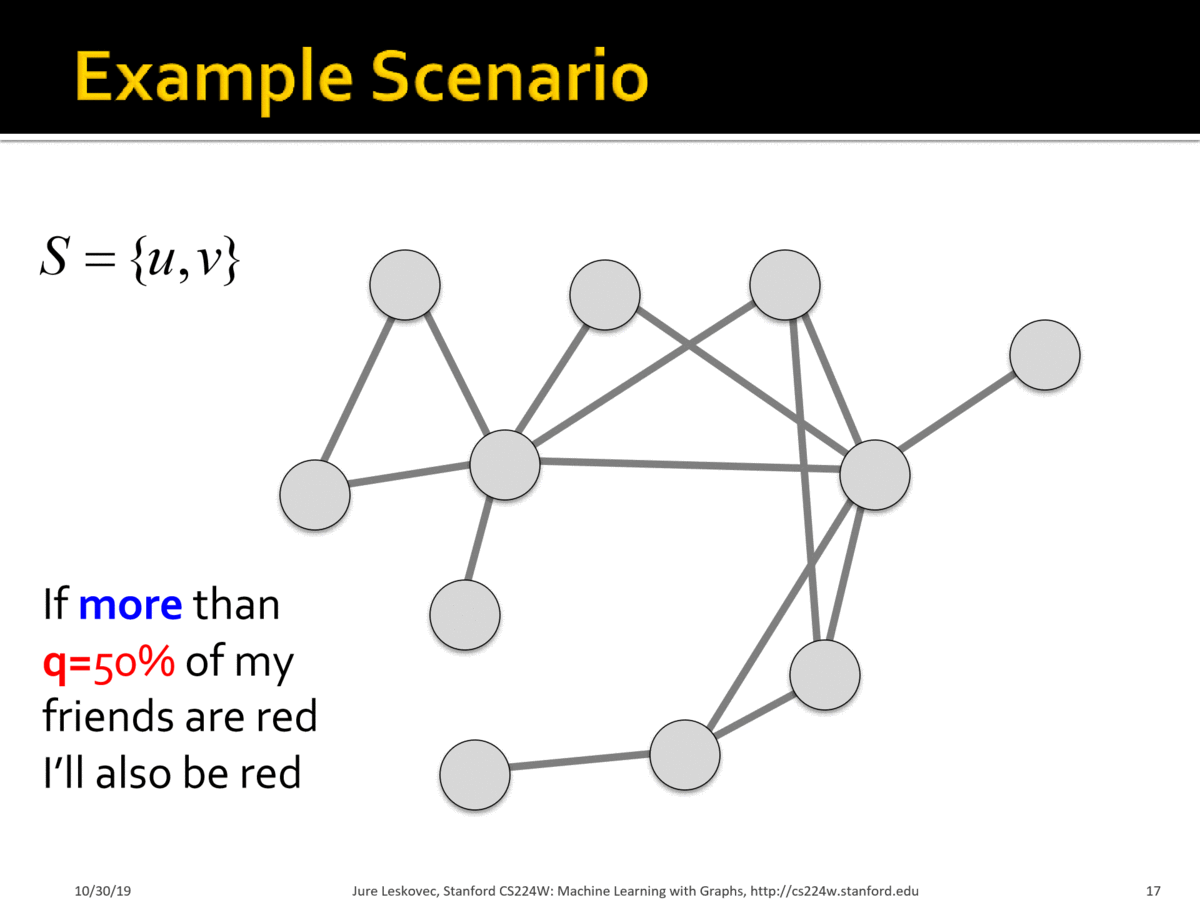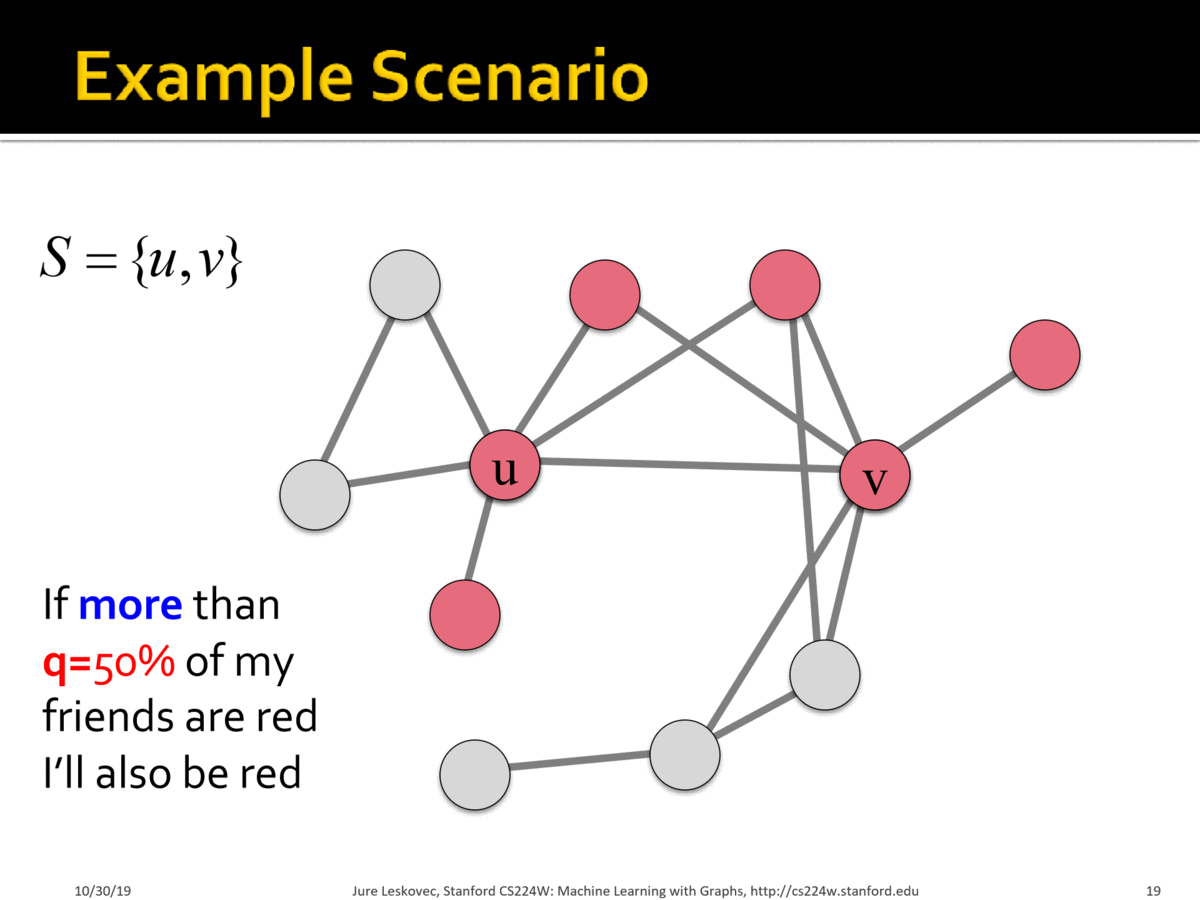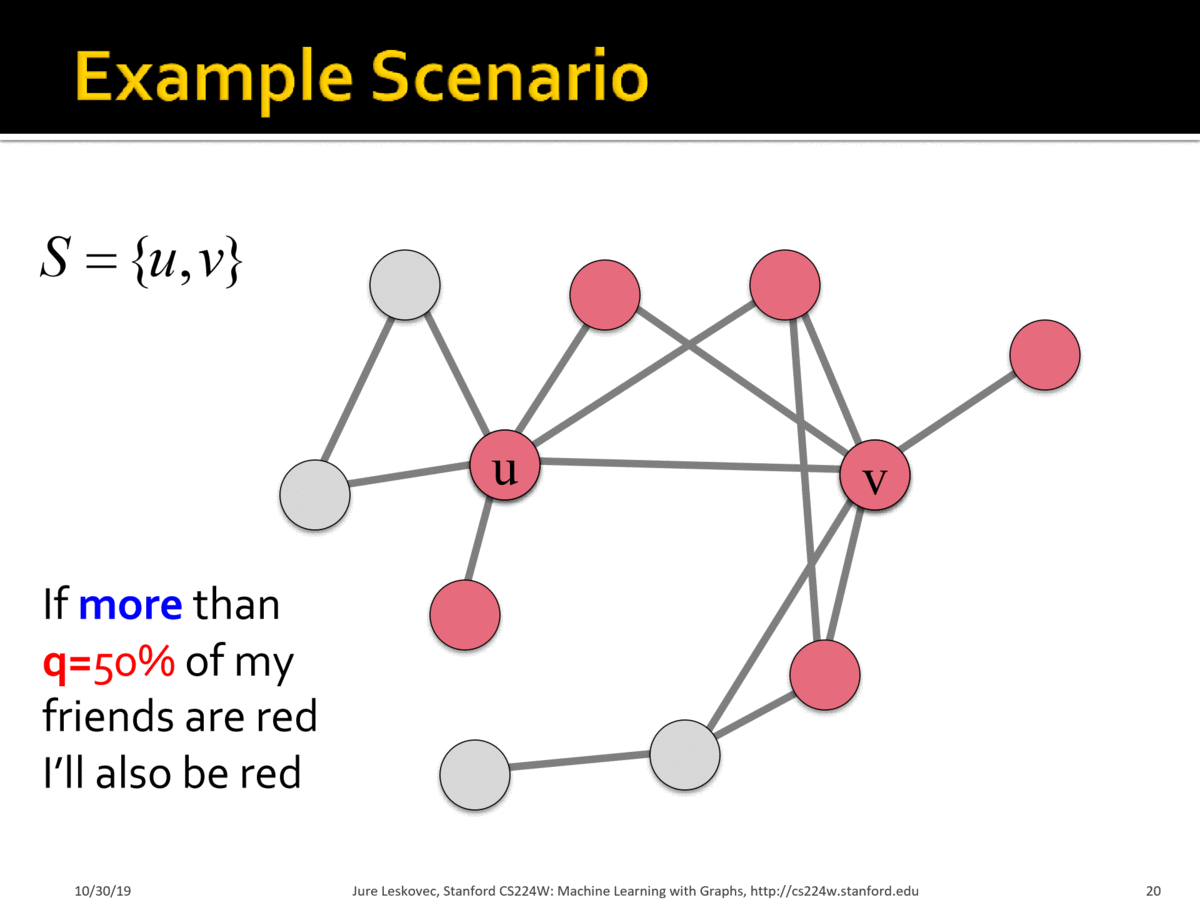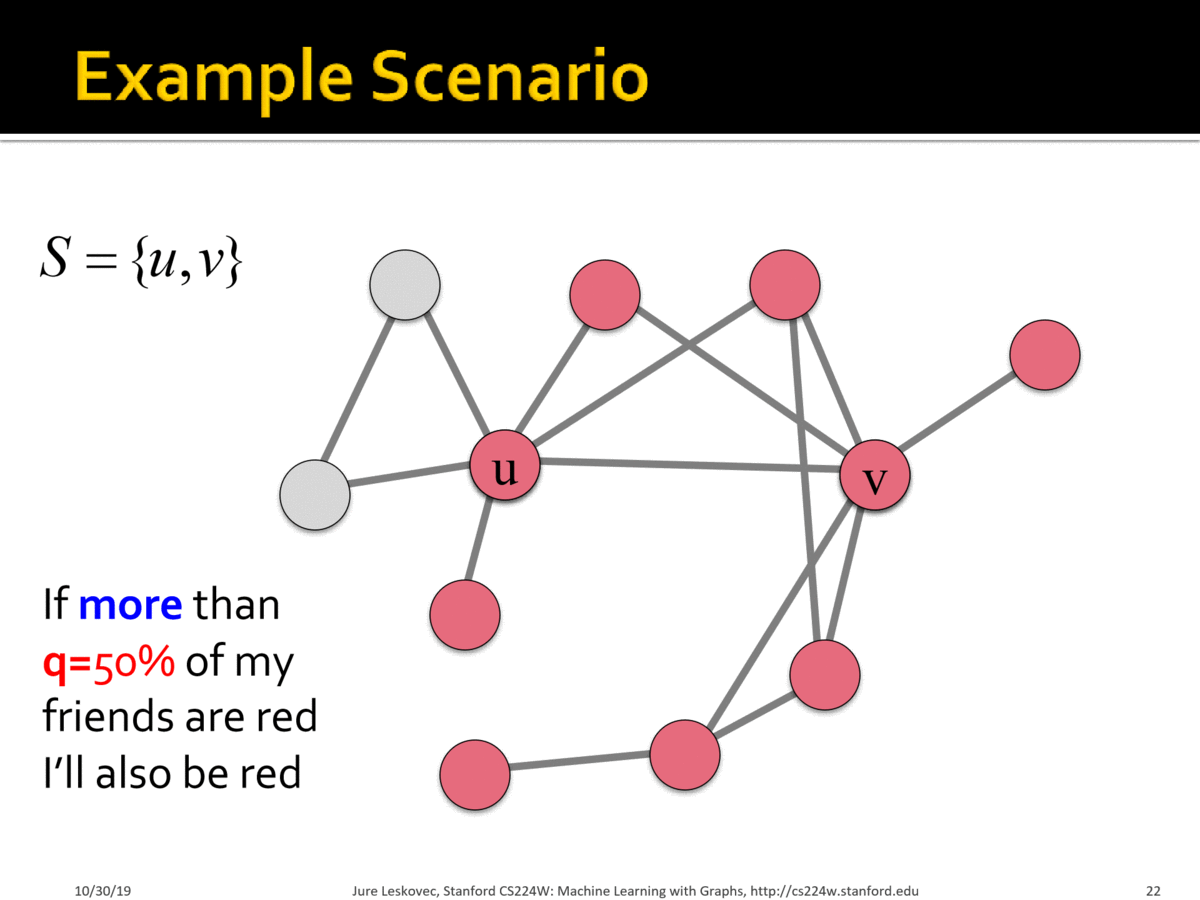
Example:
Scenario:
- Graph where all nodes start with $$B$$
- Small set $$S$$ of early adopters of $$A$$. Hardwire this set such that these nodes will persistently use $$A$$ regardless of payoff
-Set $$a=b-\epsilon$$ and $$q = 0.5$$ for a small constant $$\epsilon>0$$. Interpretation: I adopt $$A$$ if more than 50% of my neighbors adopt $$A$$.
Case Study: Modelling Protest Recruitment on social networks
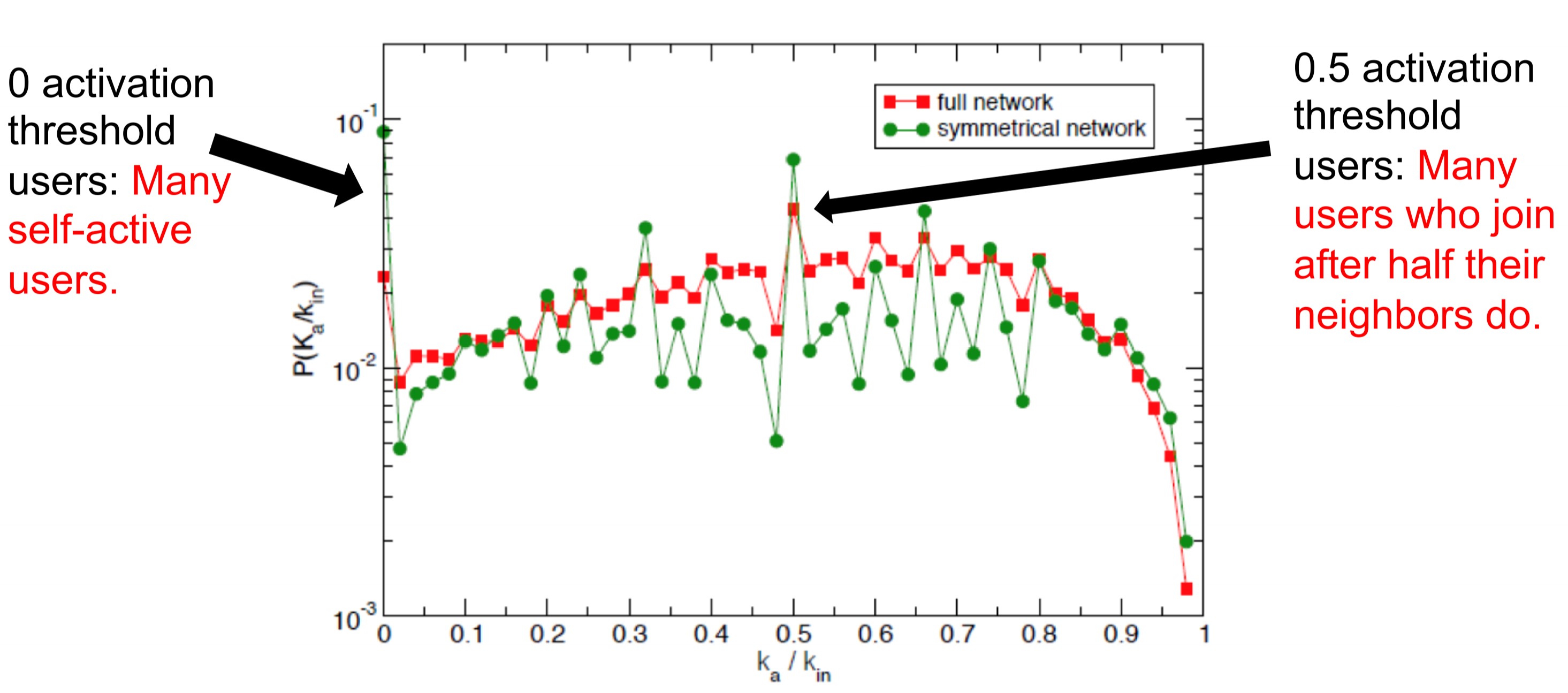
Undirected network of Twitter users. 70 identified hashtags associated with 2011 Spain anti-austerity protests. For each user (node):
- User activation time = moment when user starts tweeting protest messages
- $$k_{in}$$ = total number of neighbors at user activation time
- $$k_{a}$$ = number of activate neighbors at user activation time
- Activation threshold $$\frac{k_{a}}{k_{in}}$$ = fraction of neighbors that are active at user activation time
Key Insights:
- The distribution of activation threshold had two local peaks: i) at $$\frac{k_{a}}{k_{in}} \approx 0$$, indicating many self-active users who join with without social pressure ii) at $$\frac{k_{a}}{k_{in}} \approx 0.5$$ indicating many users join once half their neighbors have. Remainder of distribution mostly uniform.
- A "burst" of neighbors joining the movement has greater impact on users with high threshold and lesser impact on users with low threshold
- Most cascades were small
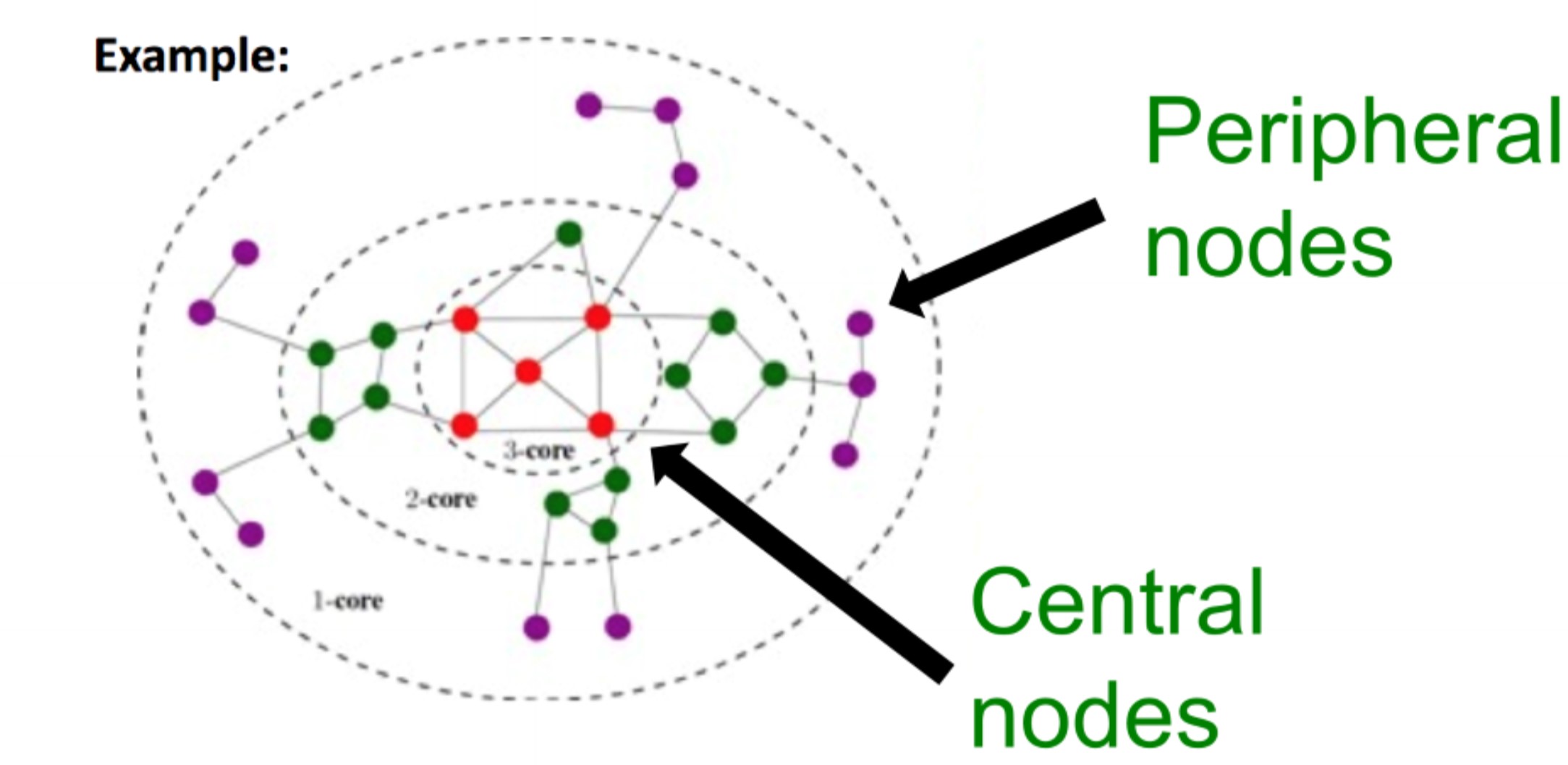
- Larger cascades were started by users with higher $$k$$-core number i.e. more central. The $$k$$-core is defined as the largest connected subgraph where every node has at least degree $$k$$ and can be evaluated by iteratively removing nodes with degree less than $$k$$.
Extending Game Theoretic Model: multi-behavior adoption
A node can adopt both behaviors and become $$AB$$ by paying a cost $$c$$. The resulting payoff matrix (without cost $$c$$ applied) is as follows:
| A | B | AB | |
|---|---|---|---|
| A | a | 0 | a |
| B | 0 | b | b |
| AB | a | b | max(a,b) |
Example: Infinite path graph
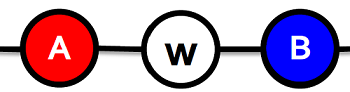
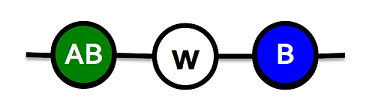
Let us examine an infinite path graph where everyone begins with behavior/product $$B$$ except for three nodes of the following cases. Let us also set $$b=1$$.
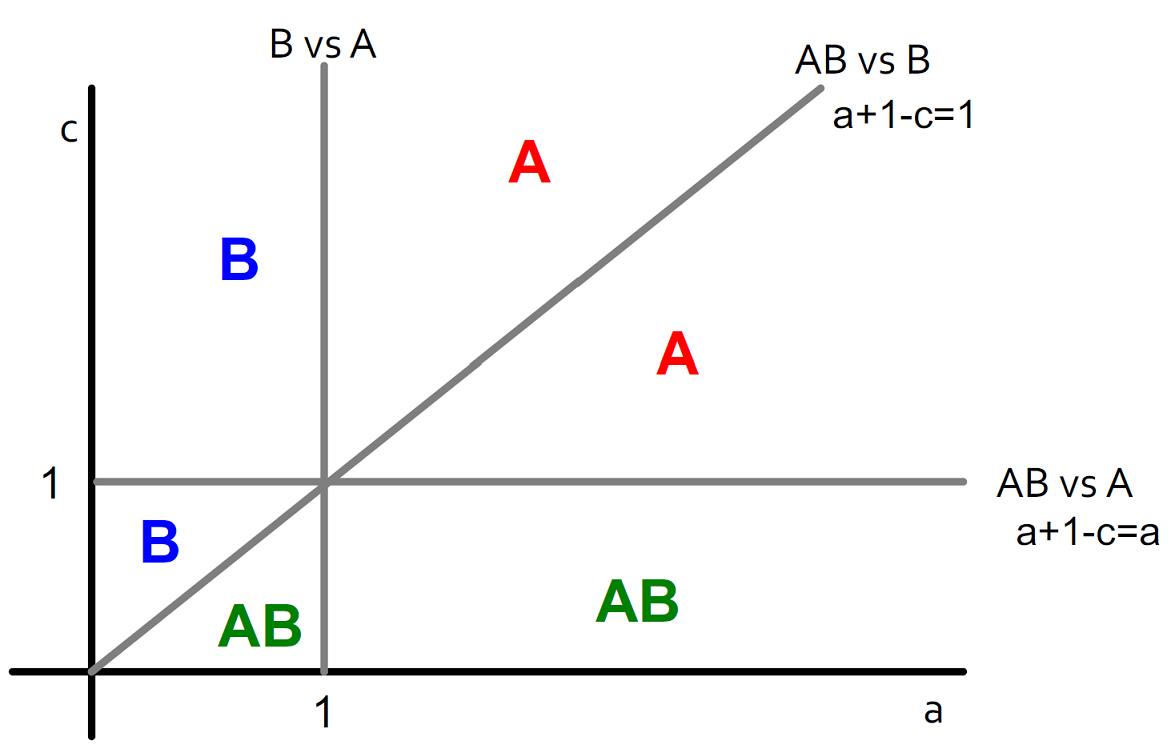
Payoffs for $$w$$: $$A: a$$, $$B: 1$$, $$AB: a+1-c$$
Payoffs for $$w$$: $$A: a$$, $$B: 1$$, $$AB: max(a, 1) + 1 -c$$
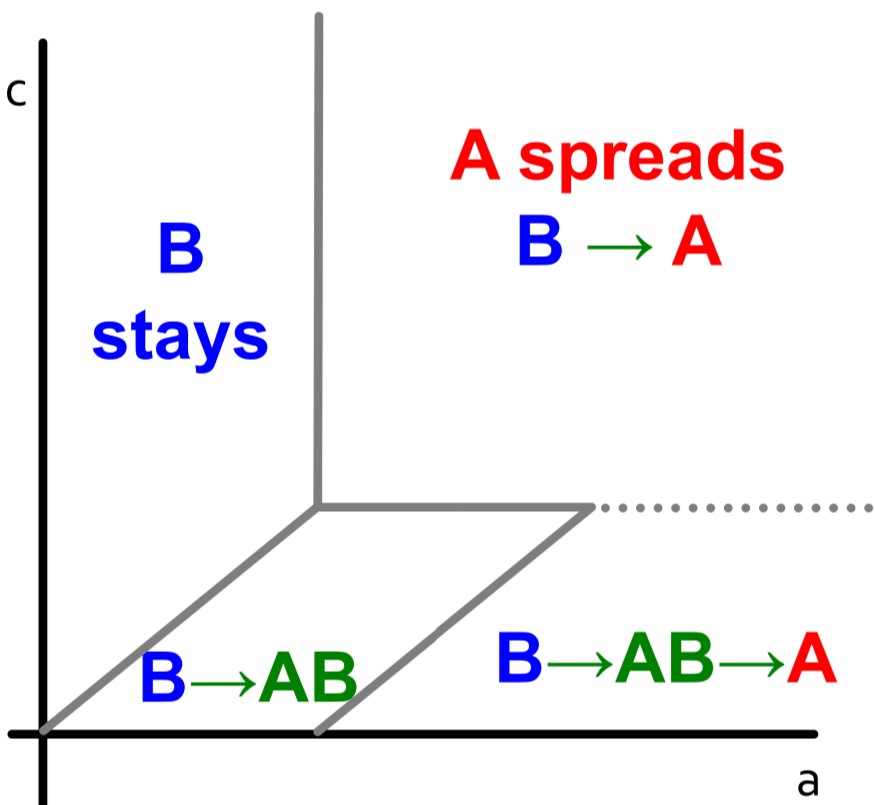
The graphs show how different regions of $$(a,c)$$ values impact the decision-based diffusion:
- B->A (Direct Conquest): If $$a$$ and $$c$$ are both high, then the cost of being compatible to both products is not worth it and conversion to $$A$$ is direct
- B->AB->A (Infiltration): If $$a$$ is high and $$c$$ is lower, users first transition to $$AB$$ before fully committing to $$A$$