Influence Maximization and Outbreak Detection (#12)

* add influence_maximization and figures, edit .gitignore to ignore jekyll cache

* fix repeated the

* change the file name with dash, add outbreak detection

*  finished outbreak detection

* proof reading done

* update with suggestions

* Add sidenote for other evaluation methods besides sketches, make Hill Climbing Algorithm more precise

.gitignore

@@ -1,4 +1,5 @@
 _site
 .sass-cache
 .DS\_Store
-config.codekit
+.jekyll-cache/
+config.codekit

index.md

@@ -2,12 +2,12 @@
 layout: post
 title: Contents
 ---
-<span class="newthought">These notes</span> form a concise introductory course on machine learning with large-scale graphs. They mirror the topics topics covered by Stanford [CS224W](https://cs224w.stanford.edu), and are written by the CS 224W TAs. 
+<span class="newthought">These notes</span> form a concise introductory course on machine learning with large-scale graphs. They mirror the topics topics covered by Stanford [CS224W](https://cs224w.stanford.edu), and are written by the CS 224W TAs.
 {% include marginnote.html id='mn-construction' note='The notes are still under construction! They will be written up as lectures continue to progress. If you find any typos, please let us know, or submit a pull request with your fixes to our [GitHub repository](https://github.com/snap-stanford/cs224w-notes).'%}
 
 You too may help make these notes better by submitting your improvements to us via [GitHub](https://github.com/snap-stanford/cs224w-notes). Note that submitting substantial improvements will result in *bonus points* being added to your overall grade!
 
-Starting with the Fall 2019 offering of CS 224W, the course covers three broad topic areas for understanding and effectively learning representations from large-scale networks: preliminaries, network methods, and machine learning with networks. Subtopics within each area correspond to individual lecture topics. 
+Starting with the Fall 2019 offering of CS 224W, the course covers three broad topic areas for understanding and effectively learning representations from large-scale networks: preliminaries, network methods, and machine learning with networks. Subtopics within each area correspond to individual lecture topics.
 
 ## Preliminaries
 
@@ -19,8 +19,8 @@ Starting with the Fall 2019 offering of CS 224W, the course covers three broad t
 
 1. [Structural Roles in Networks](): RolX, Granovetter, the Louvain algorithm
 2. [Spectral Clustering](network-methods/spectral-clustering): Graph partitions and cuts, the Laplacian, and motif clustering
-3. [Influence Maximization](): Influential sets, submodularity, hill climbing
-4. [Outbreak Detection](): CELF, lazy hill climbing
+3. [Influence Maximization](network-methods/influence-maximization): Influential sets, submodularity, hill climbing
+4. [Outbreak Detection](network-methods/outbreak-detection): CELF, lazy hill climbing
 5. [Link Analysis](): PageRank and SimRank
 6. [Network Effects and Cascading Behavior](network-methods/network-effects-and-cascading-behavior): Decision-based diffusion, probabilistic contagion, SEIZ
 7. [Network Robustness](): Power laws, preferential attachment

network-methods/influence-maximization.md

@@ -0,0 +1,154 @@
+---
+layout: post
+title: Influence Maximization
+---
+
+## Motivation
+Identification of influential nodes in a network has important practical uses. A good example is "viral marketing", a strategy that uses existing social networks to spread and promote a product. A well-engineered viral marking compaign will identify the most influential customers, convince them to adopt and endorse the product, and then spread the product in the social network like a virus.
+
+The key question is how to find the most influential set of nodes? To answer this question, we will first look at two classical cascade models:
+
+- Linear Threshold Model
+- Independent Cascade Model
+
+Then, we will develop a method to find the most influential node set in the Independent Cascade Model.
+
+## Linear Threshold Model
+In the Linear Threshold Model, we have the following setup:
+
+- A node $$v$$ has a random threshold $$\theta_{v} \sim U[0,1]$$
+- A node $$v$$ influenced by each neighbor $$w$$ according to a weight $$b_{v,w}$$, such that
+
+$$
+\sum_{w\text{ neighbor of v }} b_{v,w}\leq 1
+$$
+
+- A node $$v$$ becomes active when at least $$\theta_{v}$$ fraction of its neighbors are active. That is
+
+$$
+\sum_{w\text{ active neighbor of v }} b_{v,w}\geq\theta_{v}
+$$
+
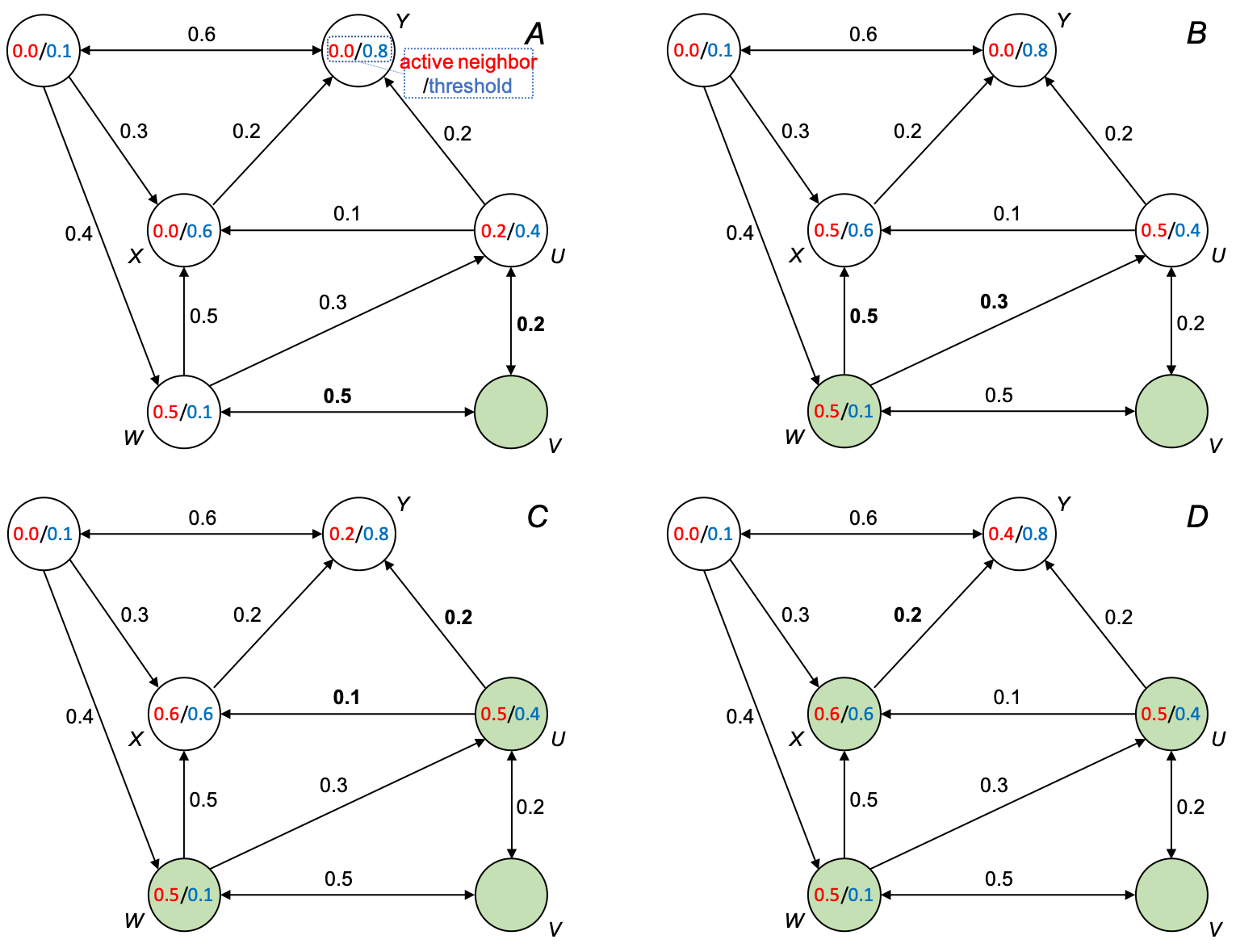
+The following figure demonstrates the process:
+
+![linear_threshold_model_demo](../assets/img/influence_maximization_linear_threshold_model_demo.png?style=centerme)
+
+*(A) node V is activated and influences W and U by 0.5 and 0.2, respectively; (B) W becomes activated and influences X and U by 0.5 and 0.3, respectively; (C) U becomes activated and influences X and Y by 0.1 and 0.2, respectively; (D) X becomes activated and influences Y by 0.2; no more nodes can be activated; process stops.*
+
+## Independent Cascade Model
+In this model, we model the influences (activation) of nodes based on probabilities in a directed graph:
+
+- Given a directed finite graph $$G=(V, E)$$
+- Given a node set $$S$$ starts with a new behavior (e.g. adopted new product and we say they are active)
+- Each edge $$(v, w)$$ has a probability $$p_{vw}$$
+- If node $$v$$ becomes active, it gets one chance to make $$w$$ active with probability $$p_{vw}$$
+- Activation spread through the network
+
+Note:
+
+- Each edge fires only once
+- If $$u$$ and $$v$$ are both active and link to $$w$$, it does not matter which tries to activate $$w$$ first
+
+## Influential Maximization (of the Independent Cascade Model)
+
+### Definitions
+- **Most influential Set of size $$k$$** ($$k$$ is a user-defined parameter) is a set $$S$$ containing $$k$$ nodes that if activated, produces the largest expected{% include sidenote.html id='note-most-influential-set' note='Why "expected cascade size"? Due to the stochastic nature of the Independent Cascade Model, node activation is a random process, and therefore, $$f(S)$$ is a random variable. In practice, we would like to compute many random simulations and then obtain the expected value $$f(S)=\frac{1}{\mid I\mid}\sum_{i\in I}f_{i}(S)$$, where $$I$$ is a set of simulations.' %} cascade size $$f(S)$$.
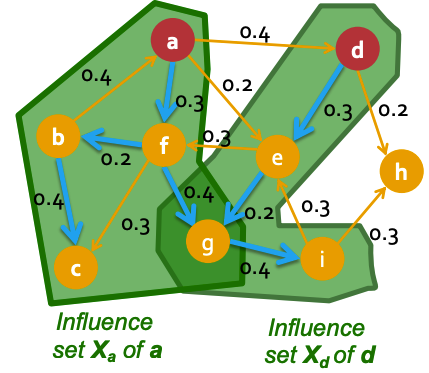
+- **Influence set $$X_{u}$$ of node $$u$$** is the set of nodes that will be eventually activated by node $$u$$. An example is shown below.
+
+![influence_set](../assets/img/influence_maximization_influence_set.png?style=centerme)
+
+*Red-colored nodes a and b are active. The two green areas enclose the nodes activated by a and b respectively, i.e. $$X_{a}$$ and $$X_{b}$$.*
+
+Note:
+- It is clear that $$f(S)$$ is the size of the union of $$X_{u}$$: $$f(S)=\mid\cup_{u\in S}X_{u}\mid$$.
+- Set $$S$$ is more influential, if $$f(S)$$ is larger
+
+### Problem Setup
+The influential maximization problem is then an optimization problem:
+
+$$
+\max_{S \text{ of size }k}f(S)
+$$
+
+This problem is NP-hard [[Kempe et al. 2003]](https://www.cs.cornell.edu/home/kleinber/kdd03-inf.pdf). However, there is a greedy approximation algorithm--**Hill Climbing** that gives a solution $$S$$ with the following approximation guarantee:
+
+$$
+f(S)\geq(1-\frac{1}{e})f(OPT)
+$$
+
+where $$OPT$$ is the globally optimal solution.
+
+### Hill Climbing
+**Algorithm:** at each step $$i$$, activate and pick the node $$u$$ that has the largest marginal gain $$\max_{u}f(S_{i-1}\cup\{u\})$$:
+
+- Start with $$S_{0}=\{\}$$
+- For $$i=1...k$$
+  - Activate node $$u\in V\setminus S_{i-1}$$ that $$\max_{u}f(S_{i-1}\cup\{u\})$$
+  - Let $$S_{i}=S_{i-1}\cup\{u\}$$
+
+**Claim:** Hill Climbing produces a solution that has the approximation guarantee $$f(S)\geq(1-\frac{1}{e})f(OPT)$$.
+
+### Proof of the Approximation Guarantee of Hill Climbing
+**Definition of Monotone:** if $$f(\emptyset)=0$$ and $$f(S)\leq f(T)$$ for all $$S\subseteq T$$, then $$f(\cdot)$$ is monotone.
+
+**Definition of Submodular:** if $$f(S\cup \{u\})-f(S)\geq f(T\cup\{u\})-f(T)$$ for any node $$u$$ and any $$S\subseteq T$$, then $$f(\cdot)$$ is submodular.
+
+**Theorem [Nemhauser et al. 1978]:**{% include sidenote.html id='note-nemhauser-theorem' note='also see this [handout](http://web.stanford.edu/class/cs224w/handouts/CS224W_Influence_Maximization_Handout.pdf)' %} if $$f(\cdot)$$ is **monotone** and **submodular**, then the $$S$$ obtained by greedily adding $$k$$ elements that maximize marginal gains satisfies
+
+$$
+f(S)\geq(1-\frac{1}{e})f(OPT)
+$$
+
+Given this theorem, we need to prove that the largest expected cascade size function $$f(\cdot)$$ is monotone and submodular.
+
+**It is clear that the function $$f(\cdot)$$ is monotone based on the definition of $$f(\cdot)$${% include sidenote.html id='note-monotone' note='If no nodes are active, then the influence is 0. That is $$f(\emptyset)=0$$. Because activating more nodes will never hurt the influence, $$f(U)\leq f(V)$$ if $$U\subseteq V$$.' %}, and we only need to prove $$f(\cdot)$$ is submodular.**
+
+**Fact 1 of Submodular Functions:** $$f(S)=\mid \cup_{k\in S}X_{k}\mid$$ is submodular, where $$X_{k}$$ is a set. Intuitively, the more sets you already have, the less new "area", a newly added set $$X_{k}$$ will provide.
+
+**Fact 2 of Submodular Functions:** if $$f_{i}(\cdot)$$ are submodular and $$c_{i}\geq0$$, then $$F(\cdot)=\sum_{i}c_{i} f_{i}(\cdot)$$ is also submodular. That is a non-negative linear combination of submodular functions is a submodular function.
+
+**Proof that $$f(\cdot)$$ is Submodular**: we run many simulations on graph G (see sidenote 1). For the simulated world $$i$$, the node $$v$$ has an activation set $$X^{i}_{v}$$, then $$f_{i}(S)=\mid\cup_{v\in S}X^{i}_{v}\mid$$ is the size of the cascades of $$S$$ for world $$i$$. Based on Fact 1, $$f_{i}(S)$$ is submodular. The expected influence set size $$f(S)=\frac{1}{\mid I\mid}\sum_{i\in I}f_{i}(S)$$ is also submodular, due to Fact 2. QED.
+
+**Evaluation of $$f(S)$$ and Approximation Guarantee of Hill Climbing In Practice:** how to evaluate $$f(S)$$ is still an open question. The estimation achieved by simulating a number of possible worlds is a good enough evaluation [[Kempe et al. 2003]](https://www.cs.cornell.edu/home/kleinber/kdd03-inf.pdf):
+
+- Estimate $$f(S)$$ by repeatedly simulating $$\Omega(n^{\frac{1}{\epsilon}})$$ possible worlds, where $$n$$ is the number of nodes and $$\epsilon$$ is a small positive real number
+- It achieves $$(1\pm \epsilon)$$-approximation to $$f(S)$$
+- Hill Climbing is now a $$(1-\frac{1}{e}-\epsilon)$$-approximation
+
+### Speed-up Hill Climbing by Sketch-Based Algorithms
+
+**Time complexity of Hill Climbing**
+
+To find the node $$u$$ that $$\max_{u}f(S_{i-1}\cup\{u\})$$ (see the algorithm above):
+
+- we need to evaluate the $$X_{u}$$ (the influence set) of each of the remaining nodes which has the size of $$O(n)$$ ($$n$$ is the number of nodes in $$G$$)
+- for each evaluation, it takes $$O(m)$$ time to flip coins for all the edges involved ($$m$$ is the number of edges in $$G$$)
+- we also need $$R$$ simulations to estimate the influence set ($$R$$ is the number of simulations/possible worlds)
+
+We will do this $$k$$ (number of nodes to be selected) times. Therefore, the time complexity of Hill Climbing is $$O(k\cdot n \cdot m \cdot R)$$, which is slow. We can use **sketches** [[Cohen et al. 2014]](https://www.microsoft.com/en-us/research/wp-content/uploads/2014/08/skim_TR.pdf) to speed up the evaluation of $$X_{u}$$ by reducing the evaluation time from $$O(m)$$ to $$O(1)$${% include sidenote.html id='note-evaluate-influence' note='Besides sketches, there are other proposed approaches for efficiently evaluating the influence function: approximation by hypergraphs [[Borgs et al. 2012]](https://arxiv.org/pdf/1212.0884.pdf), approximating Riemann sum [[Lucier et al. 2015]](https://people.seas.harvard.edu/~yaron/papers/localApproxInf.pdf), sparsification of influence networks [[Mathioudakis et al. 2011]](https://chato.cl/papers/mathioudakis_bonchi_castillo_gionis_ukkonen_2011_sparsification_influence_networks.pdf), and heuristics, such as degree discount [[Chen et al. 2009]](https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/weic-kdd09_influence.pdf).'%}.
+
+**Single Reachability Sketches**
+
+- Take a possible world $$G^{i}$$ (i.e. one simulation of the graph $$G$$ using the Independent Cascade Model)
+- Give each node a uniform random number $$\in [0,1]$$
+- Compute the **rank** of each node $$v$$, which is the **minimum** number among the nodes that $$v$$ can reach in this world.
+
+*Intuition: if $$v$$ can reach a large number of nodes, then its rank is likely to be small. Hence, the rank of node $$v$$ can be used to estimate the influence of node $$v$$ in $$G^{i}$$.*
+
+However, influence estimation based on Single Reachability Sketches (i.e. single simulation of $$G$$ ) is inaccurate. To make a more accurate estimate, we need to build sketches based on many simulations{% include sidenote.html id='note-sketches' note='This is similar to take an average of $$f_{i}(S)$$ in sidenote 1, but in this case, it is achieved by using Combined Reachability Sketches.' %}, which leads to the Combined Reachability Sketches.
+
+**Combined Reachability Sketches**
+
+In Combined Reachability Sketches, we simulate several possible worlds and keep the smallest $$c$$ values among the nodes that $$u$$ can reach in all the possible worlds.
+
+- Construct Combined Reachability Sketches:
+
+  - Generate a number of possible worlds
+  - For node $$u$$, assign uniformly distributed random numbers $$r^{i}_{v}\in[0,1]$$ to all $$(v, i)$$ pairs, where $$v$$ is the node in $$u$$'s reachable nodes set in the world $$i$$.
+  - Take the $$c$$ smallest $$r^{i}_{v}$$ as the Combined Reachability Sketches
+
+- Run Greedy for Influence Maximization:
+  - Whenever the greedy algorithm asks for the node with the largest influence, pick node $$u$$ that has the smallest value in its sketch.
+  - After $$u$$ is chosen, find its influence set $$X^{i}_{u}$$, mark the $$(v, i)$$ as infected and remove their $$r^{i}_{v}$$ from the sketches of other nodes.
+
+Note: using Combined Reachability Sketches does not provide an approximation guarantee on the true expected influence but an approximation guarantee with respect to the possible worlds considered.

network-methods/outbreak-detection.md

@@ -0,0 +1,198 @@
+---
+layout: post
+title: Outbreak Detection in Networks
+---
+
+## Introduction
+The general goal of outbreak detection in networks is that given a dynamic process spreading over a network, we want to select a set of nodes to detect the process efficiently. Outbreak detection in networks has many applications in real life. For example, where should we place sensors to quickly detect contaminations in a water distribution network? Which person should we follow on Twitter to avoid missing important stories?
+
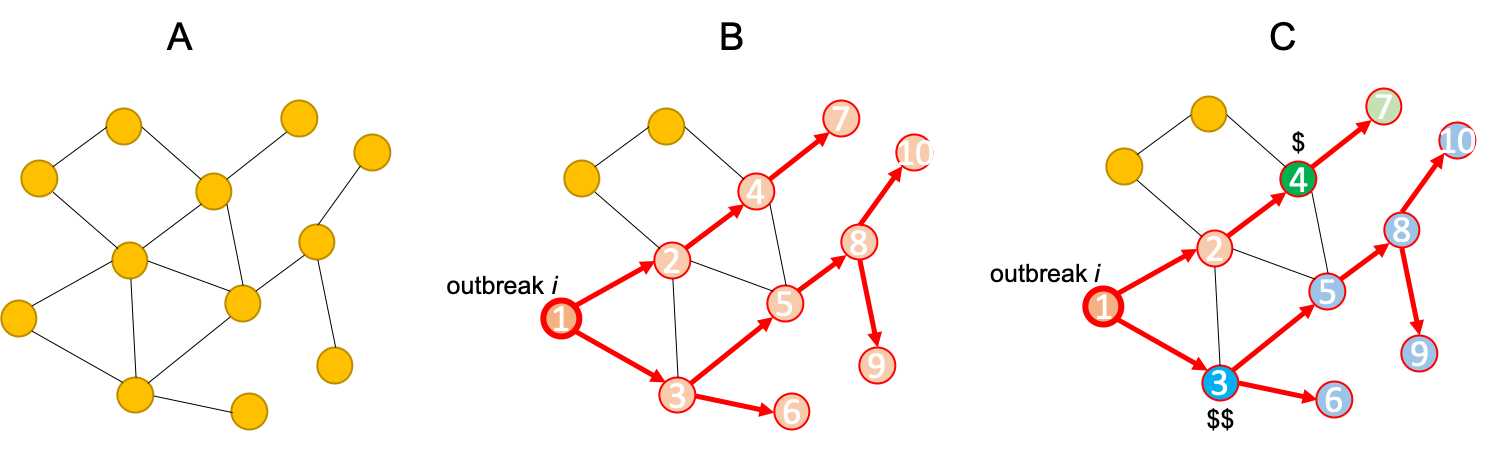
+The following figure shows the different effects of placing sensors at two different locations in a network:
+
+![sensor_placement](../assets/img/outbreak_detection_sensor_placement.png?style=centerme)
+*(A) The given network. (B) An outbreak $$i$$ starts and spreads as shown. (C) Placing a sensor at the blue position saves more people and also detects earlier than placing a sensor at the green position, though costs more.*
+
+## Problem Setup
+The outbreak detection problem is defined as below:
+- Given: a graph $$G(V,E)$$ and data on how outbreaks spread over this $$G$$ (for each outbreak $$i$$, we knew the time $$T(u,i)$$ when the outbreak $$i$$ contaminates node $$u$$).
+- Goal: select a subset of nodes $$S$$ that maximize the expected reward:
+
+$$
+\max_{S\subseteq U}f(S)=\sum_{i}p(i)\cdot f_{i}(S)
+$$
+
+$$
+\text{subject to cost }c(S)\leq B
+$$
+
+where
+
+- $$p(i)$$: probability of outbreak $$i$$ occurring
+- $$f_{i}(S)$$: rewarding for detecting outbreak $$i$$ using "sensors" $$S$${% include sidenote.html id='note-outbreak-detection-problem-setup' note='It is obvious that $$p(i)\cdot f_{i}(S)$$ is the expected reward for detecting the outbreak $$i$$' %}
+- $$B$$: total budget of placing "sensors"
+
+
+**The Reward** can be one of the following three:
+
+- Minimize the time to detection
+- Maximize the number of detected propagations
+- Minimize the number of infected people
+
+**The Cost** is context-dependent. Examples are:
+
+- Reading big blogs is more time consuming
+- Placing a sensor in a remote location is more expensive
+
+## Outbreak Detection Formalization
+
+### Objective Function for Sensor Placements
+
+Define the **penalty $$\pi_{i}(t)$$** for detecting outbreak $$i$$ at time $$t$$, which can be one of the following:{% include sidenote.html id='note-outbreak-detection-penalty-note' note='Notice: in all the three cases detecting sooner does not hurt! Formally, this means, for all three cases, $$\pi_{i}(t)$$ is monotonically nondecreasing in $$t$$.'%}
+
+- **Time to Detection (DT)**
+  - How long does it take to detect an outbreak?
+  - Penalty for detecting at time $$t$$: $$\pi_{i}(t)=t$$
+
+- **Detection Likelihood (DL)**
+  - How many outbreaks do we detect?
+  - Penalty for detecting at time $$t$$: $$\pi_{i}(0)=0$$, $$\pi_{i}(\infty)=1$${% include sidenote.html id='note-penalty-dl' note='this is a binary outcome:  $$\pi_{i}(0)=0$$ means we detect the outbreak and we pay 0 penalty, while $$\pi_{i}(\infty)=1$$ means we fail to detect the outbreak and we pay 1 penalty. That is we do not incur any penalty if we detect the outbreak in finite time, otherwise we incur penalty 1.'%}
+
+- **Population Affected (PA)**
+  - How many people/nodes get infected during an outbreak?
+  - Penalty for detecting at time $$t$$: $$\pi_{i}(t)=$$ number of infected nodes in the outbreak $$i$$ by time $$t$$
+
+The objective **reward function $$f_{i}(S)$$ of a sensor placement $$S$$** is defined as penalty reduction:
+
+$$
+f_{i}(S)=\pi_{i}(\infty)-\pi_{i}(T(S,i))
+$$
+
+where $$T(S,i)$$ is the time when the set of "sensors" $$S$$ detects the outbreak $$i$$.
+
+### Claim 1: $$f(S)=\sum_{i}p(i)\cdot f_{i}(S)$$ is monotone{% include sidenote.html id='note-monotone' note='For the definition of monotone, see [Influence Maximization](influence-maximization)' %}
+Firstly, we do not reduce the penalty, if we do not place any sensors. Therefore, $$f_{i}(\emptyset)=0$$ and $$f(\emptyset)=\sum_{i}p(i)\cdot f_{i}(\emptyset)=0$$.
+
+Secondly, for all $$A\subseteq B\subseteq V$$ ($$V$$ is all the nodes in $$G$$), $$T(A,i)\geq T(B,i)$$, and
+
+$$
+\begin{align*}
+f_{i}(A)-f_{i}(B)&=\pi_{i}(\infty)-\pi_{i}(T(A,i))-[\pi_{i}(\infty)-\pi_{i}(T(B,i))]\\
+&=\pi_{i}(T(B,i))-\pi_{i}(T(A,i))
+\end{align*}
+$$
+
+Because $$\pi_{i}(t)$$ is monotonically nondecreasing in $$t$$ (see sidenote 2), $$f_{i}(A)-f_{i}(B)<0$$. Therefore, $$f_{i}(S)$$ is nondecreasing. It is obvious that $$f(S)=\sum_{i}p(i)\cdot f_{i}(S)$$ is also nondecreasing, since $$p(i)\geq 0$$.
+
+Hence, $$f(S)=\sum_{i}p(i)\cdot f_{i}(S)$$ is monotone.
+
+
+### Claim 2: $$f(S)=\sum_{i}p(i)\cdot f_{i}(S)$$ is submodular{% include sidenote.html id='note-submodular' note='For the definition of submodular, see [Influence Maximization](influence-maximization)' %}
+This is to proof for all $$A\subseteq B\subseteq V$$ $$x\in V \setminus B$$:
+
+$$
+f(A\cup \{x\})-f(A)\geq f(B\cup\{x\})-f(B)
+$$
+
+There are three cases when sensor $$x$$ detects the outbreak $$i$$:
+1. $$T(B,i)\leq T(A, i)<T(x,i)$$ ($$x$$ detects late): nobody benefits. That is $$f_{i}(A\cup\{x\})=f_{i}(A)$$ and $$f_{i}(B\cup\{x\})=f_{i}(B)$$. Therefore, $$f(A\cup \{x\})-f(A)=0= f(B\cup\{x\})-f(B)$$
+2. $$T(B, i)\leq T(x, i)<T(A,i)$$ ($$x$$ detects after $$B$$ but before $$A$$): $$x$$ only helps to improve the solution of $$A$$ but not $$B$$. Therefore, $$f(A\cup \{x\})-f(A)\geq 0 = f(B\cup\{x\})-f(B)$$
+3. $$T(x, i)<T(B,i)\leq T(A,i)$$ ($$x$$ detects early): $$f(A\cup \{x\})-f(A)=[\pi_{i}(\infty)-\pi_{i}(T(x,t))]-f_{i}(A)$$$$ \geq [\pi_{i}(\infty)-\pi_{i}(T(x,t))]-f_{i}(B) = f(B\cup\{x\})-f(B)$${% include sidenote.html id='note-submodularity-proof1' note='Inequality is due to the nondecreasingness of $$f_{i}(\cdot)$$, i.e. $$f_{i}(A)\leq f_{i}(B)$$ (see Claim 1).'%}
+
+Therefore, $$f_{i}(S)$$ is submodular. Because $$p(i)\geq 0$$, $$f(S)=\sum_{i}p(i)\cdot f_{i}(S)$$ is also submodular.{% include sidenote.html id='note-submodularity-proof1' note='Fact: a non-negative linear combination of submodular functions is a submodular function.'%}
+
+We know that the Hill Climbing algorithm works for optimizing problems with nondecreasing submodular objectives. However, it does not work well in this problem:
+
+- Hill Climbing only works for the cases that each sensor costs the same. For this problem, each sensor has cost $$c(s)$$.
+- Hill Climbing is also slow: at each iteration, we need to re-evaluate marginal gains of all nodes. The run time is $$O(\mid V\mid\cdot k)$$ for placing $$k$$ sensors.
+
+Hence, we need a new fast algorithm that can handle cost constraints.
+
+## CELF: Algorithm for Optimziating Submodular Functions Under Cost Constraints
+### Bad Algorithm 1: Hill Climbing that ignores the cost
+**Algorithm**
+
+- Ignore sensor cost $$c(s)$$
+- Repeatedly select sensor with highest marginal gain
+- Do this until the budget is exhausted
+
+**This can fail arbitrarily bad!** Example:
+- Given $$n$$ sensors and a budget $$B$$
+- $$s_{1}$$: reward $$r$$, cost $$B$$
+- $$s_{2}$$,..., $$s_{n}$$: reward $$r-\epsilon$$, cost $$\epsilon$$ ($$\epsilon$$ is an arbitrary positive small number)
+- Hill Climbing always prefers $$s_{1}$$ to other cheaper sensors, resulting in an arbitrarily bad solution with reward $$r$$ instead of the optimal solution with reward $$\frac{B(r-\epsilon)}{\epsilon}$$, when $$\epsilon \rightarrow 0$$.
+
+### Bad Algorithm 2: optimization using benefit-cost ratio
+**Algorithm**
+- Greedily pick the sensor $$s_{i}$$ that maximizes the benefit to cost ratio until the budget runs out, i.e. always pick
+
+$$
+s_{i}=\arg\max_{s\in(V\setminus A_{i-1})}\frac{f(A_{i-1}\cup\{s\})-f(A_{i-1})}{c(s)}
+$$
+
+**This can fail arbitrarily bad!** Example:
+- Given 2 sensors and a budget $$B$$
+- $$s_{1}$$: reward $$2\epsilon$$, cost $$\epsilon$$
+- $$s_{2}$$: reward $$B$$, cost $$B$$
+- Then the benefit ratios for the first selection are: 2 and 1, respectively
+- This algorithm will pick $$s_{1}$$ and then cannot afford $$s_{2}$$, resulting in an arbitrarily bad solution with reward $$2\epsilon$$ instead of the optimal solution $$B$$, when $$\epsilon \rightarrow 0$$.
+
+### Solution: CELF (Cost-Effective Lazy Forward-selection)
+**CELF** is a two-pass greedy algorithm [[Leskovec et al. 2007]](https://www.cs.cmu.edu/~jure/pubs/detect-kdd07.pdf):
+- Get solution $$S'$$ using unit-cost greedy (Bad Algorithm 1)
+- Get solution $$S''$$ using benefit-cost greedy (Bad Algorithm 2)
+- Final solution $$S=\arg\max[f(S'), f(S'')]$$
+
+**Approximation Guarantee**
+- CELF achieves $$\frac{1}{2}(1-\frac{1}{e})$$ factor approximation.
+
+CELF also uses a lazy evaluation of $$f(S)$$ (see below) to speedup Hill Climbing.
+
+## Lazy Hill Climbing: Speedup Hill Climbing
+
+### Intuition
+- In Hill Climbing, in round $$i+1$$, we have picked $$S_{i}=\{S_{1},...,S_{i}\}$$ sensors. Now, pick $$s_{i+1}=\arg\max_{u}f(S_{i}\cup \{u\})-f(S_{i})$$
+- By submodularity $$f(S_{i}\cup\{u\})-f(S_{i})\geq f(S_{j}\cup\{u\})-f(S_{j})$$ for $$i<j$$.
+- Let $$\delta_{i}(u)=f(S_{i}\cup\{u\})-f(S_{i})$$ and $$\delta_{j}(u)=f(S_{j}\cup\{u\})-f(S_{j})$$ be the marginal gains. Then, we can use $$\delta_{i}$$ as upper bound on $$\delta_{j}$$ for ($$j>i$$)
+
+### Lazy Hill Climbing Algorithm:
+- Keep an ordered list of marginal benefits $$\delta_{i-1}$$ from previous iteration
+- Re-evaluate $$\delta_{i}$$ only for the top nodes
+- Reorder and prune from the top nodes
+
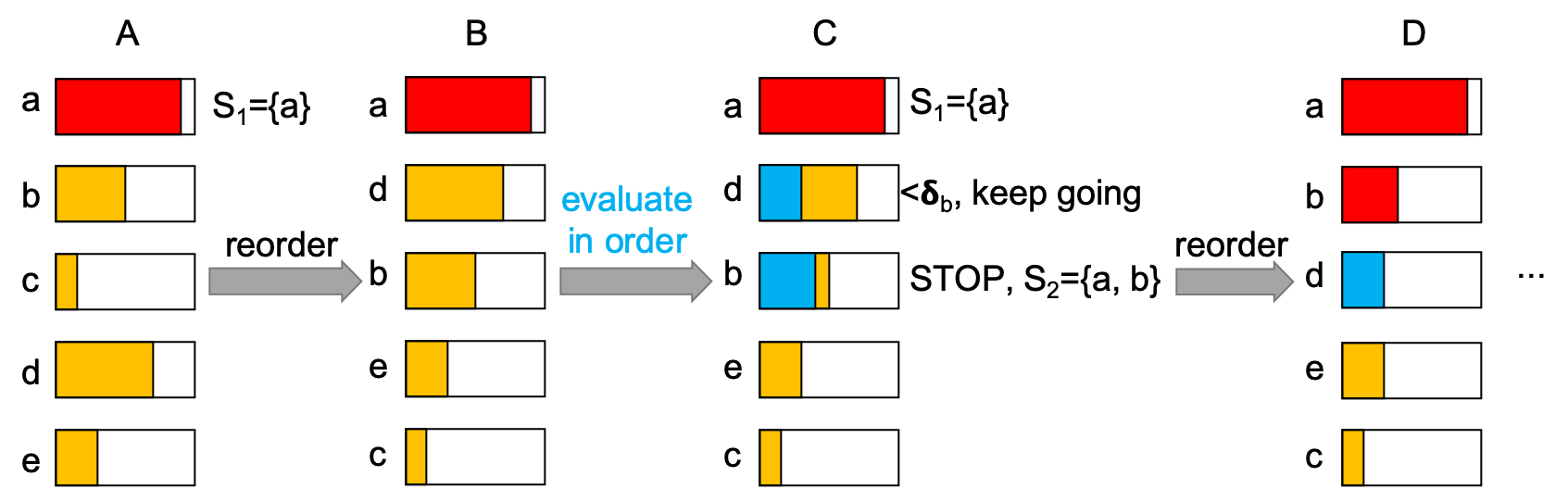
+The following figure show the process.
+
+![lazy_evaluation](../assets/img/outbreak_detection_lazy_evaluation.png?style=centerme)
+
+*(A) Evaluate and pick the node with the largest marginal gain $$\delta$$. (B) reorder the marginal gain for each sensor in decreasing order. (C) Re-evaluate the $$\delta$$s in order and pick the possible best one by using previous $$\delta$$s as upper bounds. (D) Reorder and repeat.*
+
+Note: the worst case of Lazy Hill Climbing has the same time complexity as normal Hill Climbing. However, it is on average much faster in practice.
+
+## Data-Dependent Bound on the Solution Quality
+
+### Introduction
+- Value of the bound depends on the input data
+- On "easy data", Hill Climbing may do better than the $$(1-\frac{1}{e})$$ bound for submodular functions
+
+### Data-Dependent Bound
+Suppose $$S$$ is some solution to $$f(S)$$ subjected to $$\mid S \mid\leq k$$, and $$f(S)$$ is monotone and submodular.
+
+- Let $$OPT={t_{i},...,t_{k}}$$ be the optimal solution
+- For each $$u$$ let $$\delta(u)=f(S\cup\{u\})-f(S)$$
+- Order $$\delta(u)$$ so that $$\delta(1)\geq \delta(2)\geq...$$
+- Then, the **data-dependent bound** is $$f(OPT)\leq f(S)+\sum^{k}_{i=1}\delta(i)$$
+
+Proof:{% include sidenote.html id='note-data-dependent-bound-proof' note='For the first inequality, see [the lemma in 3.4.1 of this handout](http://web.stanford.edu/class/cs224w/handouts/CS224W_Influence_Maximization_Handout.pdf). For the last inequality in the proof: instead of taking $$t_{i}\in OPT$$ of benefit $$\delta(t_{i})$$, we take the best possible element $$\delta(i)$$, because we do not know $$t_{i}$$.'%}
+
+$$
+\begin{align*}
+  f(OPT)&\leq f(OPT\cup S)\\
+  &=f(S)+f(OPT\cup S)-f(S)\\
+  &\leq f(S)+\sum^{k}_{i=1}[f(S\cup\{t_{i}\})-f(S)]\\
+  &=f(S)+\sum^{k}_{i=1}\delta(t_{i})\\
+  &\leq f(S)+\sum^{k}_{i=1}\delta(i)
+\end{align*}
+$$
+
+Note:
+
+- This bound hold for the solution $$S$$ (subjected to $$\mid S \mid\leq k$$) of any algorithm having the objective function $$f(S)$$ monotone and submodular.
+- The bound is data-dependent, and for some inputs it can be very "loose" (worse than $$(1-\frac{1}{e})$$)