3 changed files with 97 additions and 0 deletions
Split View
Diff Options
-
+97 -0blogContent/posts/programming/CS -Theory-Exam-2-Review.md
-
BINblogContent/posts/programming/media/CSTHEORY/DFAMinimalProof.png
-
BINblogContent/posts/programming/media/CSTHEORY/DFAMinimalTable.png
+ 97
- 0
blogContent/posts/programming/CS -Theory-Exam-2-Review.md
View File
| @ -0,0 +1,97 @@ | |||
| This a very high level review post that I am making for myself and other people taking CS Theory. | |||
| If you want to lean about the theory behind the content in this blog post I recommed looking else where. | |||
| This post will cover how to solve typical problems relating to topics covered by my second CS Theory exam. | |||
| ## Myhill-Nerode Theorem | |||
| ### Definition | |||
| L is regular if and only if it has a finite index. The index is the maximum number of elements thar are pairwise distibguishable. | |||
| Two strings are said to be pairwise distinguishable if you can append something to both of the strings and it makes one string | |||
| accepted by the language and the other string non-accepting. | |||
| The size of an index set X equals the number of equivalence classes it has. Each element in the language is accepted by only | |||
| one equivalence class. | |||
| ### Problem Approach | |||
| Prove that language L is regular. | |||
| 1) Define a set X which is infinite in size - this doesn;t necesarrily need to be in the language. | |||
| 2) Make a general argument that show that each element in X is pairwise distinguishable. | |||
| Pick any two elements x, y in X and show that if you append z to them one is accepted by the language and | |||
| the other is not in the language. | |||
| ### Example | |||
| Prove the following language is non-regular: | |||
| $$ | |||
| L={ww^r | w \in {0,1}^*} | |||
| $$ | |||
| answer: | |||
| 1) | |||
| $$ | |||
| X = {(01)^i | i \geq 0} | |||
| $$ | |||
| Pick any 2 elements of X and show pairwise distinguishable | |||
| $$ | |||
| x = (01)^i, y = (01)^j | i \neq j | |||
| $$ | |||
| suppose we pick | |||
| $$ | |||
| z = (10)^i\\ | |||
| xz \in L\\ | |||
| yz \notin L | |||
| $$ | |||
| ## DFA minimization algorithm | |||
| Types of Problems: | |||
| - Prove DFA is minimal | |||
| - Minimize the DFA | |||
| The argument for DFA minimization comes from the Myhill-Nerode theorem. Given | |||
| a DFA, if you can form a set of strings which represent each state and they are all | |||
| pairwise distinguishable, then the DFA is minimal with that many states. | |||
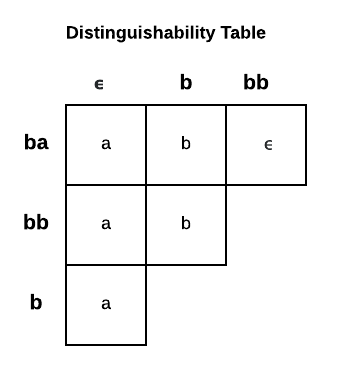
| ### Prove DFA is minimal | |||
| For these types of problems you simply construct a table and show that each state is pairwise distinguishable. | |||
| To show pairwise distinguishability you have to show that there exists a string where if appened to one element | |||
| makes it accepted by the language but pushes the other string out of the language. | |||
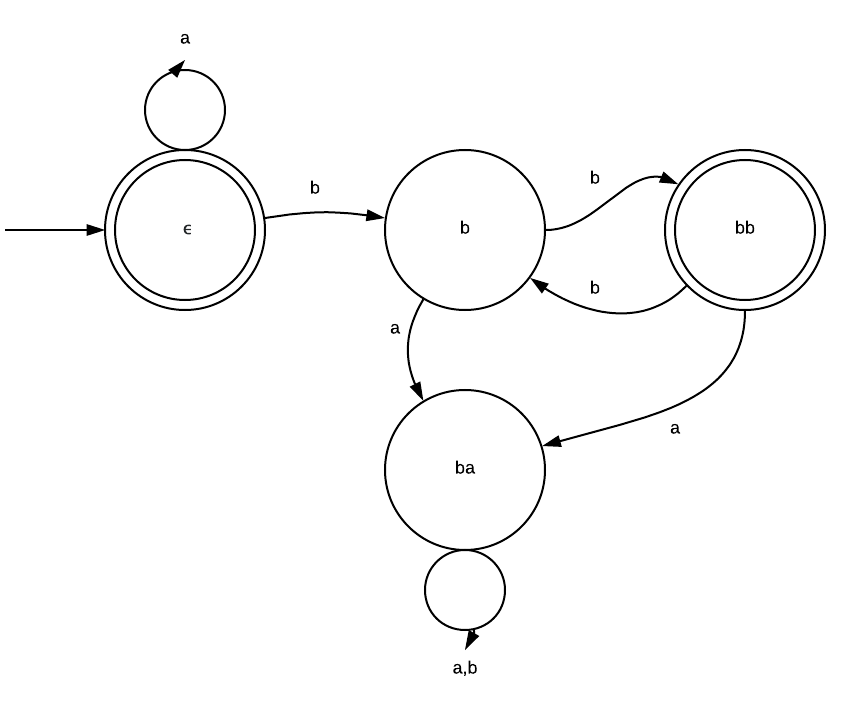
| ex: Prove the following DFA is minimal. | |||
|  | |||
| $$ | |||
| X = {\epsilon, b, bb, ba} | |||
| $$ | |||
|  | |||
| ### Minimize the DFA | |||
| ## Pumping lemma for regular languages | |||
| ## Context-free grammars, closure properties for CFLs | |||
| ## Parse trees, ambiguity | |||
| ## Chomsky Normal Form | |||
| ## Pushdown automata | |||
| ## Construction to convert CFG to a PDA | |||