|
|
|
@ -0,0 +1,395 @@ |
|
|
|
If you have ever taken a computer science class you probably |
|
|
|
know what the fibonacci sequence is and how to calculate it. |
|
|
|
For those who don't know: [Fibonacci](https://en.wikipedia.org/wiki/Fibonacci) |
|
|
|
is a sequence of numbers starting with 0,1 whose next number is the sum |
|
|
|
of the two previous numbers. After having multiple of my CS classes |
|
|
|
give lectures and homeworks on the Fibonacci sequence; I decided |
|
|
|
to write a blog post going over |
|
|
|
the 4 main ways of calculating the nth term of the Fibonacci sequence. |
|
|
|
In addition to providing the python code for calculating the nth perm of the sequence, a proof for their validity |
|
|
|
and an analysis of their time complexities both mathematically and empirically will |
|
|
|
be examined. |
|
|
|
|
|
|
|
# Slow Recursive Definition |
|
|
|
|
|
|
|
By the definition of the Fibonacci sequence, it is the most natural to write it as |
|
|
|
a recursive definition. |
|
|
|
|
|
|
|
```Python |
|
|
|
def fib(n): |
|
|
|
if n == 0 or n == 1: |
|
|
|
return n |
|
|
|
return fib(n-1) + fib(n-2) |
|
|
|
``` |
|
|
|
|
|
|
|
##Time Complexity |
|
|
|
|
|
|
|
Observing that each call has two recursive calls we can place an upper bound on this |
|
|
|
function as $O(2^n)$. However, if we solve this recurrence we can place a tight bound for time complexity. |
|
|
|
|
|
|
|
We can write a recurrence for the number of times fib is called: |
|
|
|
|
|
|
|
$$ |
|
|
|
F(1) = 1\\ |
|
|
|
F(n) = F(n-1) + F(n-2)\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
Next, we replace F(n) with $a^n$ since we want to find rate of exponential growth. |
|
|
|
|
|
|
|
$$ |
|
|
|
a^n = a^{n-1} + a^{n-2}\\ |
|
|
|
\frac{a^n}{a^{n-2}} = \frac{a^{n-1} + a^{n-2}}{a^{n-2}}\\ |
|
|
|
a^2 = a + 1\\ |
|
|
|
a = \frac{1 \pm sqrt(5)}{2}\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
From this calculation we can conclude that F(n) $\in \Theta 1.681^n$. We don't have to worry about |
|
|
|
the negative root since it would not be asymptotically relevant by the definition of $\Theta$. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
## Measured Performance |
|
|
|
|
|
|
|
Here is a graph of the actual performance that I observed from this recursive definition of Fibonacci. |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
# Accumulation Solution |
|
|
|
|
|
|
|
The problem with the previous recursive solution is that you had to recalculate certain |
|
|
|
terms of fibonacci a ton of times. A summation variable would help us avoid this problem. |
|
|
|
You could write this solution using a simple loop or dynamic programming |
|
|
|
, however, I chose to use recursion to demonstrate that it's recursion which made the first |
|
|
|
problem slow. |
|
|
|
|
|
|
|
|
|
|
|
```Python |
|
|
|
def fibHelper(n, a, b): |
|
|
|
if n == 0: |
|
|
|
return a |
|
|
|
elif n == 1: |
|
|
|
return b |
|
|
|
return fibHelper(n-1, b, a+b) |
|
|
|
|
|
|
|
|
|
|
|
def fibIterative(n): |
|
|
|
return fibHelper(n, 0, 1) |
|
|
|
``` |
|
|
|
|
|
|
|
In this code example, fibHelper is a method which accumulates the previous two terms. |
|
|
|
The fibIterative is a wrapper method which sets the two initial terms equal to 0 and 1 |
|
|
|
representing the fibonacci sequence. At first it may not be obvious that fibIterative(n) |
|
|
|
is equivalent to fib(n). To demonstrate that these two are in fact equivalent, I broke this |
|
|
|
into two inductive proofs. |
|
|
|
|
|
|
|
## Proof for Fib Helper |
|
|
|
**Lemma:** For any n $\epsilon$ N if n $>$ 1 then |
|
|
|
$fibHelper(n, a, b) = fibHelper(n - 1, a, b) + fibHelper(n - 2, a, b)$. |
|
|
|
|
|
|
|
**Proof via Induction** |
|
|
|
|
|
|
|
**Base Case**: n = 2: |
|
|
|
$$ |
|
|
|
LHS = fibHelper(2, a, b)\\ |
|
|
|
= fibHelper(1, b, a + b) = a + b\\ |
|
|
|
RHS = fibHelper(2 -1, a, b) + fibHelper(2-2, a, b)\\ |
|
|
|
= a + b\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
**Inductive Step:** |
|
|
|
|
|
|
|
Assume proposition is true for all n and show n+1 follows. |
|
|
|
|
|
|
|
$$ |
|
|
|
RHS=fibHelper(n+1;a,b)\\ |
|
|
|
= fibHelper(n;b,a+b)\\ |
|
|
|
=fibHelper(n-1;b,a+b) + fibHelper(n-2;b,a+b)\\ |
|
|
|
=fibHelper(n;a,b) + fibHelper(n-1;a,b)\\ |
|
|
|
=LHS\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
$\Box$ |
|
|
|
|
|
|
|
## Proof That fibIterative = Fib |
|
|
|
|
|
|
|
**Lemma:** For any n $\in$ N, $fib(n)$ = $fibIterative(n, 0, 1)$ |
|
|
|
|
|
|
|
**Proof via Strong Induction** |
|
|
|
|
|
|
|
**Base Case**: n = 0: |
|
|
|
$$ |
|
|
|
fibIterative(0, 0, 0) = 0\\ |
|
|
|
= fib(0) |
|
|
|
$$ |
|
|
|
|
|
|
|
**Base Case**: n = 1: |
|
|
|
$$ |
|
|
|
fibIterative(1, 0, 0) = 1\\ |
|
|
|
= fib(1) |
|
|
|
$$ |
|
|
|
|
|
|
|
**Inductive Step:** |
|
|
|
|
|
|
|
Assume proposition is true for all n and show n+1 follows. |
|
|
|
|
|
|
|
$$ |
|
|
|
fib(n+1) = fib(n) + fib(n-1)\\ |
|
|
|
= fibHelper(n, 0, 1) + fibHelper(n+1, 0 ,1) \quad\text{I.H}\\ |
|
|
|
= fibHelper(n+1, 0, 1) \quad\text{from result in previous proof}\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
$\Box$ |
|
|
|
|
|
|
|
|
|
|
|
## Time Complexity |
|
|
|
|
|
|
|
Suppose that we wish to solve for the time complexity in terms of the number of additions needed to be |
|
|
|
computed. Based on fibHelper we can see that it performs one addition every recursive call. |
|
|
|
We can now form a recurrence for time complexity. |
|
|
|
|
|
|
|
$$ |
|
|
|
T(0) = 0\\ |
|
|
|
T(1) = 0\\ |
|
|
|
T(n) = 1 + T(n-1)\\ |
|
|
|
T(n) = n-1\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
From this recurrence we can say that fibHelper $\in \Theta(n)$. |
|
|
|
|
|
|
|
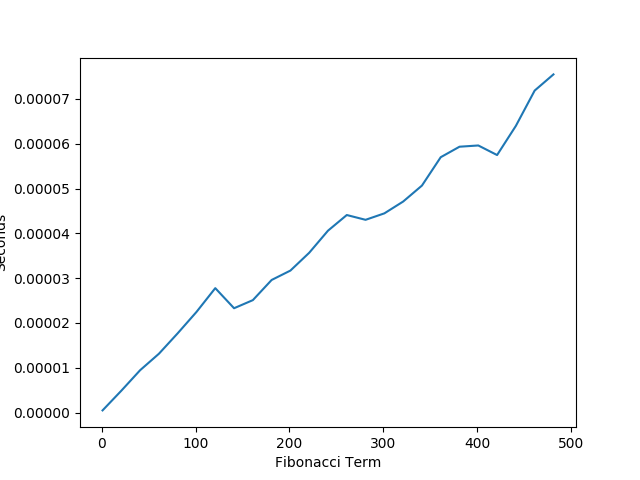
## Measured Performance |
|
|
|
|
|
|
|
Notice how much faster this solution is compared to the original recursive solution for |
|
|
|
Fibonacci. |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# Matrix Solution |
|
|
|
|
|
|
|
We can actually get better than linear for performance for Fibonacci while still using |
|
|
|
recursion. However, to do so we need to know this fact: |
|
|
|
|
|
|
|
$$ |
|
|
|
\begin{bmatrix} |
|
|
|
1 & 1\\ |
|
|
|
1 & 0 |
|
|
|
\end{bmatrix}^n = |
|
|
|
\begin{bmatrix} |
|
|
|
F_{n+1} & F_n\\ |
|
|
|
F_n & F{n-1} |
|
|
|
\end{bmatrix}^n |
|
|
|
$$ |
|
|
|
|
|
|
|
Without any tricks, raising a matrix to a power n times would not get |
|
|
|
us better than linear performance. However, if we use the [Exponentiation by Squaring](https://en.wikipedia.org/wiki/Exponentiation_by_squaring) |
|
|
|
method, we can expect to see logarithmic time. Since two spots in the matrix are always equal, |
|
|
|
I represented the matrix as an array with only three elements to reduce the space and |
|
|
|
computations required. |
|
|
|
|
|
|
|
|
|
|
|
```Python |
|
|
|
def multiply(a,b): |
|
|
|
product = [0,0,0] |
|
|
|
product[0] = a[0]*b[0] + a[1]*b[1] |
|
|
|
product[1] = a[0]*b[1] + a[1]*b[2] |
|
|
|
product[2] = a[1]*b[1] + a[2]*b[2] |
|
|
|
return product |
|
|
|
|
|
|
|
|
|
|
|
def power(l, k): |
|
|
|
if k == 1: |
|
|
|
return l |
|
|
|
temp = power(l, k//2) |
|
|
|
if k%2 == 0: |
|
|
|
return multiply(temp, temp) |
|
|
|
else: |
|
|
|
return multiply(l, multiply(temp, temp)) |
|
|
|
|
|
|
|
|
|
|
|
def fibPower(n): |
|
|
|
l = [1,1,0] |
|
|
|
return power(l, n)[1] |
|
|
|
``` |
|
|
|
|
|
|
|
|
|
|
|
## Time Complexity |
|
|
|
|
|
|
|
For this algorithm, lets solve for the time complexity as the number of additions and multiplications required. |
|
|
|
|
|
|
|
Since we are always multiplying two 2x2 matrices, that operation is constant time. |
|
|
|
|
|
|
|
$$ |
|
|
|
T_{multiply} = 9 |
|
|
|
$$ |
|
|
|
|
|
|
|
Solving for the time complexity of fib power is slightly more complicated. |
|
|
|
$$ |
|
|
|
T_{power}(1) = 0\\ |
|
|
|
T_{power}(n) = T(\left\lfloor\dfrac{n}{2}\right\rfloor) + T_{multiply}\\ |
|
|
|
= T(\left\lfloor\dfrac{n}{2}\right\rfloor) + 9\\ |
|
|
|
= T(\left\lfloor\dfrac{n}{2*2}\right\rfloor) + 9 + 9\\ |
|
|
|
= T(\left\lfloor\dfrac{n}{2*2*2}\right\rfloor) + 9+ 9 + 9\\ |
|
|
|
T_{power}(n) = T(\left\lfloor\dfrac{n}{2^k}\right\rfloor) + 9k\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
let $k=k_0$ such that $\left\lfloor\dfrac{n}{2^{k_0}}\right\rfloor = 1$ |
|
|
|
|
|
|
|
$$ |
|
|
|
\left\lfloor\dfrac{n}{2^{k_0}}\right\rfloor = 1 \rightarrow 1 \leq \frac{n}{2^{k_0}} < 2\\ |
|
|
|
\rightarrow 2^{k_0} \leq n < 2^{k_0 +1}\\ |
|
|
|
\rightarrow k_0 \leq lg(n) < k_0+1\\ |
|
|
|
\rightarrow k_0 = \left\lfloor lg(n)\right\rfloor\\ |
|
|
|
T_{power}(n) = T(1) + 9*\left\lfloor lg(n)\right\rfloor\\ |
|
|
|
T_{power}(n) = 9*\left\lfloor\ lg(n)\right\rfloor\\ |
|
|
|
T_{fibPower}(n) = T_{power}(n)\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
Now we can state that $fibPower(n) \in \Theta(log(n))$. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
## Inductive Proof for Matrix Method |
|
|
|
|
|
|
|
I would like to now prove that this matrix identity is valid since it is not at first obvious. |
|
|
|
|
|
|
|
**Lemma:** For any n $\epsilon$ N if n $>$ 0 then |
|
|
|
$$ |
|
|
|
\begin{bmatrix} |
|
|
|
1 & 1\\ |
|
|
|
1 & 0 |
|
|
|
\end{bmatrix}^n = |
|
|
|
\begin{bmatrix} |
|
|
|
F_{n+1} & F_n\\ |
|
|
|
F_n & F{n-1} |
|
|
|
\end{bmatrix}^n |
|
|
|
$$ |
|
|
|
|
|
|
|
Let |
|
|
|
|
|
|
|
$$ |
|
|
|
A= |
|
|
|
\begin{bmatrix} |
|
|
|
1 & 1\\ |
|
|
|
1 & 0 |
|
|
|
\end{bmatrix}^n |
|
|
|
$$ |
|
|
|
|
|
|
|
**Base Case:** n = 1 |
|
|
|
$$ |
|
|
|
A^1= |
|
|
|
\begin{bmatrix} |
|
|
|
1 & 1\\ |
|
|
|
1 & 0 |
|
|
|
\end{bmatrix}^n = |
|
|
|
\begin{bmatrix} |
|
|
|
F_{2} & F_2\\ |
|
|
|
F_2 & F_{0} |
|
|
|
\end{bmatrix}^n |
|
|
|
$$ |
|
|
|
|
|
|
|
**Inductive Step:** Assume proposition is true for n, show n+1 follows |
|
|
|
$$ |
|
|
|
A^{n+1}= |
|
|
|
\begin{bmatrix} |
|
|
|
1 & 1\\ |
|
|
|
1 & 0 |
|
|
|
\end{bmatrix} |
|
|
|
\begin{bmatrix} |
|
|
|
F_{n+1} & F_n\\ |
|
|
|
F_n & F{n-1} |
|
|
|
\end{bmatrix}^n\\ |
|
|
|
= \begin{bmatrix} |
|
|
|
F_{n+1} + F_n & F_n + F_{n-1}\\ |
|
|
|
F_{n+1} & F_{n} |
|
|
|
\end{bmatrix}\\ |
|
|
|
= \begin{bmatrix} |
|
|
|
F_{n+2} & F_{n+1}\\ |
|
|
|
F_{n+1} & F_{n} |
|
|
|
\end{bmatrix}\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
$\Box$ |
|
|
|
|
|
|
|
|
|
|
|
## Measured Performance |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
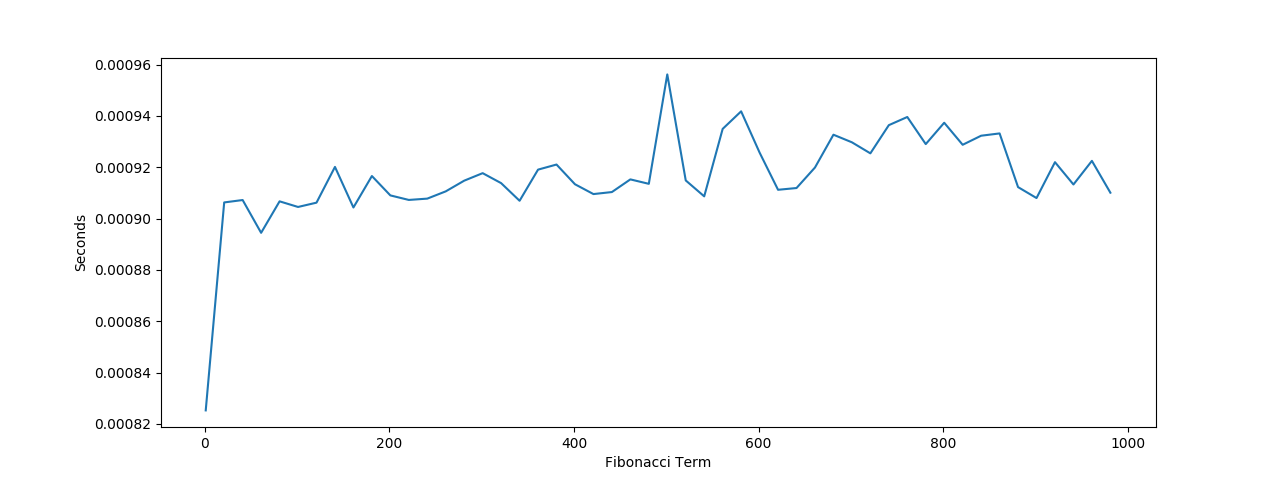
As expected by our mathematical calculations, the algorithm appears to be running in |
|
|
|
logarithmic time. |
|
|
|
|
|
|
|
## Measured Performance With Large Numbers |
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
When calculating the fibonacci term for extremely large numbers despite having a polynomial |
|
|
|
time complexity, the space required to compute each Fibonacci term grows exponentially. Since our |
|
|
|
performance is only pseudo-polynomial we see a degrade in our performance when calculating |
|
|
|
large terms of the fibonacci sequence. |
|
|
|
|
|
|
|
The one amazing thing to point out here is that despite calculating the 10,000 term of Fibonacci, |
|
|
|
this algorithm is nearly 400 times faster than the recursive algorithm when calculating |
|
|
|
the 30th term of Fibonacci. |
|
|
|
|
|
|
|
|
|
|
|
# Closed Form Definition |
|
|
|
|
|
|
|
It is actually possible to calculate Fibonacci in constant time using Binet's Formula. |
|
|
|
|
|
|
|
$$ |
|
|
|
F_n = \frac{(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n}{\sqrt{5}} |
|
|
|
$$ |
|
|
|
|
|
|
|
```Python |
|
|
|
def fibClosedFormula(n): |
|
|
|
p = ((1+ math.sqrt(5))/2)**n |
|
|
|
v = ((1-math.sqrt(5))/2)**n |
|
|
|
return (p-v)/math.sqrt(5) |
|
|
|
``` |
|
|
|
|
|
|
|
## Derivation of Binet's Formula |
|
|
|
|
|
|
|
Similar to when we were calculating the time complexity of the basic recursive definition |
|
|
|
, we want to start by finding the two roots of the equation in terms of exponents. |
|
|
|
|
|
|
|
$$ |
|
|
|
a^n = a^{n-1} + a^{n-2}\\ |
|
|
|
\frac{a^n}{a^{n-2}} = \frac{a^{n-1} + a^{n-2}}{a^{n-2}}\\ |
|
|
|
a^2 = a + 1\\ |
|
|
|
0 = a^2 - a - 1\\ |
|
|
|
a = \frac{1 \pm sqrt(5)}{2}\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
Since there are two roots to the equation, the solution of $F_n$ is going to be |
|
|
|
a linear combination of the two roots. |
|
|
|
|
|
|
|
|
|
|
|
$$ |
|
|
|
F_n = c_1(\frac{1 + \sqrt{5}}{2})^n + c_2(\frac{1 - \sqrt{5}}{2})^n |
|
|
|
$$ |
|
|
|
|
|
|
|
Fact: $F_1$ = 1 |
|
|
|
|
|
|
|
$$ |
|
|
|
F_1 = 1\\ |
|
|
|
= c_1(\frac{1 + \sqrt{5}}{2}) + c_2(\frac{1 - \sqrt{5}}{2})\\ |
|
|
|
= \frac{c_1}{2} + \frac{c_2}{2} + \frac{c_1\sqrt{5}}{2} - \frac{c_2\sqrt{5}}{2}\\ |
|
|
|
$$ |
|
|
|
|
|
|
|
Let $c_1 = \frac{1}{\sqrt{5}}$, |
|
|
|
Let $c_2 = \frac{-1}{\sqrt{5}}$ |
|
|
|
|
|
|
|
$$ |
|
|
|
F_n = \frac{1}{\sqrt(5)}((\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n)\\ |
|
|
|
= \frac{(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n}{\sqrt{5}} |
|
|
|
$$ |
|
|
|
|
|
|
|
## Time Complexity |
|
|
|
|
|
|
|
Since we managed to find the closed form of the fibonacci sequence we can expect to see constant performance. |
|
|
|
|
|
|
|
## Measured Performance |
|
|
|
|
|
|
|
 |
jrtechs
6 years ago
