Added csci-331 exam 2 review notes to blog.

blogContent/posts/data-science/csci-331-review-2.md

@@ -0,0 +1,170 @@
+# Ch 4: Iterative improvement
+
+## Simulated annealing
+
+Idea: escape local maxima by allowing some bad moves but gradually decrease their size and frequency.
+This is similar to gradient descent.
+Idea comes from making glass where you start very hot and then slowely cool down the temperature.
+
+
+## Beam search
+
+Idea: keep k states instead of 1; choose top k of their successors.
+
+Problem: quite often all k states end up on same local hill. This can somewhat be overcome by randomly choosing k states but, favoring the good ones. 
+
+
+## Genetic algorithms
+
+Inspired by Charles Darwin's theory of evolution.
+The algorithm is an extension of local beam search with cuccessors generated from pairs of individuals rather than a successor function.
+
+![GA overview](media/exam1/gaOverview.png)
+
+![Genetic Algorithm Pseudo Code](media/exam1/gaAlgo.png)
+
+
+# Ch 6: Constraint satisfaction problems
+
+Ex CSP problems:
+
+- assignment
+- timetabling
+- hardware configuration
+- spreadsheets
+- factory scheduling
+- Floor-planning
+
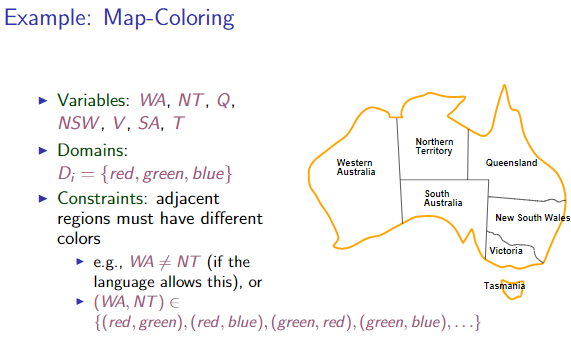
+## Problem formulation
+
+![CSP formulation ex](media/exam2/cspEx.PNG)
+
+### Variables
+
+Elements in the problem.
+
+### Domains
+
+Possible values from domain $D_i$, try to be mathematical when formulating.
+
+### Constraints
+
+Constraints on the variables specifying what values from the domain they may have.
+
+Types of constraints:
+
+- Unary: Constraints involving single variable
+- Binary: Constraints involving pairs of variables
+- Higher-order: Constraints involving 3 or more variables
+- Preferences: Where you favor one value in the domain more than another. This is mostly used for constrained optimization problems.
+
+## Constraint graphs
+
+Nodes in graph are variables, arcs show constraints
+
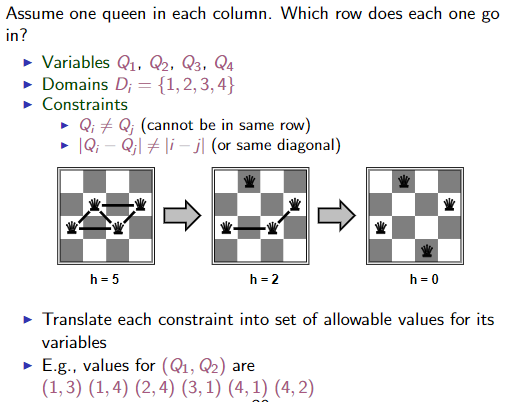
+## Backtracking
+
+![Backtracking graph](media/exam2/backtracking.PNG)
+
+### Minimum remaining value
+
+![](media/exam2/mrv.PNG)
+
+Choose the variable wit the fewest legal values left.
+
+### Degree heuristic
+
+![](media/exam2/degree.PNG)
+
+Tie-breaker for minimum remaining value heuristic.
+Choose the variable with the most constraints on remaining variables. 
+
+### Least constraining value
+
+Choose the least constraining value: one that rules out fewest values in remaining variables.
+
+![lsv](media/exam2/lsv.PNG)
+
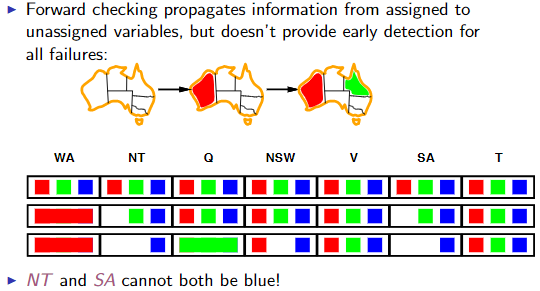
+### Forward checking
+
+Keep track of remaining legal values for unassigned variables and terminate search when any variable has no legal values left.
+This will help reduce how many nodes in the tree you have to expand. 
+
+![forward checking](media/exam2/forwardChecking.PNG)
+
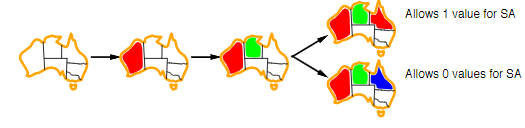
+### Constraint propagation
+
+![](media/exam2/constraintProp.PNG)
+
+### Arc consistency
+
+![](media/exam2/arc.PNG)
+
+### Tree structured CSPs
+
+Theorem: if constraint graph has no loops, the CSP ca be solved in $O(n*d^2)$ time.
+General CSP is $O(d^n)$
+
+![](media/exam2/treeCSP.PNG)
+
+## Connections to tree search, iterative improvement
+
+To apply this to hill-climbing, you select any conflicted variable and then use a min-conflicts heuristic
+to choose a value that violates the fewest constraints.
+
+![](media/exam2/nQueens.PNG)
+
+
+# CH 13: Uncertainty
+
+## Basic theory and terminology
+
+### Probability space
+
+The probability space $\omega$ is all possible outcomes.
+A dice roll has 6 possible outcomes.
+
+### Atomic Event
+
+An atomic event w is a single element from the probability space.
+$w \in \omega$
+Ex: rolling a dice of 4
+The probability of w is between [0,1].
+
+
+
+### Event
+
+An event A is any subset of the probability space $\omega$
+The probability of an event is the sum of the probabilities of the atom events in the event.
+
+Ex: probability of rolling a even number dice is 1/2.
+
+```
+P(die roll odd) = P(1)+P(2)+3P(5) = 1/6+1/6+1/6 = 1/2
+```
+
+### Random variable
+
+Is a function from some sample points to some range. eg reals or booleans.
+eg: P(Even = true)
+
+## Prior probability
+
+Probabilities based given one or more events.
+Ex: probability cloudy and fall = 0.72.
+
+Given two variables with two possible assignments, we could represent all the information in a 2x2 matrix.
+
+## Conditional Probability
+
+Probabilities based within a event.
+Eg: P(tired | monday) = .9. 
+
+## Bayes rule
+
+![](media/exam2/bay.PNG)
+
+## Independence
+
+![](media/exam2/independence.PNG)