Segmenting images with quad trees post

blogContent/posts/photography/segmenting-images-with-quadtrees.md

@@ -0,0 +1,323 @@
+Alright, this post is long overdue; today, we are using quadtrees to partition images. I wrote this code before writing the post on [generic quad trees](https://jrtechs.net/data-science/implementing-a-quadtree-in-python). However, I haven't had time to turn it into a blog post until now. Let's dive right into this post where I use a custom quadtree implementation and OpenCV to partition images.
+
+But first, why might you want to use quadtrees on an image? In the last post on quadtrees, we discussed how quadtrees get used for efficient spatial search.
+That blog post covered point quadtrees where every element in the quadtree got represented as a single fixed point.
+With images, each node in the quadtree represents a region of the image.
+We can generate our quadtree in a similar fashion where instead of dividing based on how many points are in the region, we can divide based on the contrast in the cell.
+The end goal is to create partitions that minimize the contrast contained within each node/cell.
+By doing so, we can compress our image while preserving essential details.
+
+With that said, let's jump into the python code. Like most of my open CV projects, we start by importing the standard dependencies, loading a test image, and then defining some helper functions that easily display images in notebooks.
+The full Jupyter notebook for this post is in my [Random Scripts repository](https://github.com/jrtechs/RandomScripts/tree/master/notebooks) on Github.
+
+
+```python
+# Open cv library
+import cv2
+
+# matplotlib for displaying the images 
+from matplotlib import pyplot as plt
+import matplotlib.patches as patches
+
+import random
+import math
+import numpy as np
+
+img = cv2.imread('night2.jpg')
+
+def printI(img):
+    fig= plt.figure(figsize=(20, 20))
+    rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
+    plt.imshow(rgb)
+    
+    
+def printI2(i1, i2):
+    fig= plt.figure(figsize=(20, 10))
+    ax1 = fig.add_subplot(1,2,1)
+    ax1.imshow(cv2.cvtColor(i1, cv2.COLOR_BGR2RGB))
+    ax2 = fig.add_subplot(1,2,2)
+    ax2.imshow(cv2.cvtColor(i2, cv2.COLOR_BGR2RGB))
+```
+
+The test image is a long exposure shot of a street light with a full moon in the background. Notice that the moon and streetlight's overexposed nature blow them out, creating a star beam effect.
+We would expect to retain details in the moon and telephone pole when compressing the image. 
+
+```python
+printI(img)
+```
+
+![image of moon and street light](media/quadtree/output_3_0.png)
+
+Like our last implementation of a quadtree, a node is simply a representation of a spatial region.
+In our case, it is the top-left point of the image, followed by its width and height.
+To divide our image, we need to get a sense of node "purity."
+We are using the mean squared error of the pixels to determine that.
+Additionally, we are doing a weighted average of the color layers, favoring the green layer the most.
+Why we are favoring the green layer can be a point of future blog posts, but it has to do with the quantum efficiency of silicon to different types of light.
+I added normalization to our error function by dividing it by a large number; this makes it easier to tune the resulting hyperparameter in the end.
+
+```python
+ class Node():
+    def __init__(self, x0, y0, w, h):
+        self.x0 = x0
+        self.y0 = y0
+        self.width = w
+        self.height = h
+        self.children = []
+
+    def get_width(self):
+        return self.width
+    
+    def get_height(self):
+        return self.height
+    
+    def get_points(self):
+        return self.points
+    
+    def get_points(self, img):
+        return img[self.x0:self.x0 + self.get_width(), self.y0:self.y0+self.get_height()]
+    
+    def get_error(self, img):
+        pixels = self.get_points(img)
+        b_avg = np.mean(pixels[:,:,0])
+        b_mse = np.square(np.subtract(pixels[:,:,0], b_avg)).mean()
+    
+        g_avg = np.mean(pixels[:,:,1])
+        g_mse = np.square(np.subtract(pixels[:,:,1], g_avg)).mean()
+        
+        r_avg = np.mean(pixels[:,:,2])
+        r_mse = np.square(np.subtract(pixels[:,:,2], r_avg)).mean()
+        
+        e = r_mse * 0.2989 + g_mse * 0.5870 + b_mse * 0.1140
+        
+        return (e * img.shape[0]* img.shape[1])/90000000
+```
+
+After we have our nodes, we can create our quadtree data structure.
+As a design decision, the image gets stored in the quadtree where the nodes only contain partitioning information and not the image itself.
+To recursively parse the tree or display it, we merely need to pass the image pointer around rather than have copies of the image at each node of the tree.
+Additionally, we add two visualization methods to the quadtree class. One that displays a wireframe view of the nodes, the other that visualizes each leaf node by rendering that region's average color.
+
+
+```python
+class QTree():
+    def __init__(self, stdThreshold, minPixelSize, img):
+        self.threshold = stdThreshold
+        self.min_size = minPixelSize
+        self.minPixelSize = minPixelSize
+        self.img = img
+        self.root = Node(0, 0, img.shape[0], img.shape[1])
+
+    def get_points(self):
+        return img[self.root.x0:self.root.x0 + self.root.get_width(), self.root.y0:self.root.y0+self.root.get_height()]
+    
+    def subdivide(self):
+        recursive_subdivide(self.root, self.threshold, self.minPixelSize, self.img)
+    
+    def graph_tree(self):
+        fig = plt.figure(figsize=(10, 10))
+        plt.title("Quadtree")
+        c = find_children(self.root)
+        print("Number of segments: %d" %len(c))
+        for n in c:
+            plt.gcf().gca().add_patch(patches.Rectangle((n.y0, n.x0), n.height, n.width, fill=False))
+        plt.gcf().gca().set_xlim(0,img.shape[1])
+        plt.gcf().gca().set_ylim(img.shape[0], 0)
+        plt.axis('equal')
+        plt.show()
+        return
+
+    def render_img(self, thickness = 1, color = (0,0,255)):
+        imgc = self.img.copy()
+        c = find_children(self.root)
+        for n in c:
+            pixels = n.get_points(self.img)
+            # grb
+            gAvg = math.floor(np.mean(pixels[:,:,0]))
+            rAvg = math.floor(np.mean(pixels[:,:,1]))
+            bAvg = math.floor(np.mean(pixels[:,:,2]))
+
+            imgc[n.x0:n.x0 + n.get_width(), n.y0:n.y0+n.get_height(), 0] = gAvg
+            imgc[n.x0:n.x0 + n.get_width(), n.y0:n.y0+n.get_height(), 1] = rAvg
+            imgc[n.x0:n.x0 + n.get_width(), n.y0:n.y0+n.get_height(), 2] = bAvg
+
+        if thickness > 0:
+            for n in c:
+                # Draw a rectangle
+                imgc = cv2.rectangle(imgc, (n.y0, n.x0), (n.y0+n.get_height(), n.x0+n.get_width()), color, thickness)
+        return imgc
+```
+
+The recursive subdivision of a quadtree is very similar to that of a standard decision tree.
+We define two stopping criteria: node size and contrast.
+Like a decision tree, creating nodes that are too small is pedantic because it doesn't abstract the image and overfits.
+With an image, if we let our nodes become one pixel in size, it effectively just becomes the original image.
+Regarding contrast, if there is a lot of contrast, we want to continue dividing, where if there is little contrast, we want to stop dividing-- preserving global features of the image while throwing away local details.
+
+```python
+def recursive_subdivide(node, k, minPixelSize, img):
+
+    if node.get_error(img)<=k:
+        return
+    w_1 = int(math.floor(node.width/2))
+    w_2 = int(math.ceil(node.width/2))
+    h_1 = int(math.floor(node.height/2))
+    h_2 = int(math.ceil(node.height/2))
+
+
+    if w_1 <= minPixelSize or h_1 <= minPixelSize:
+        return
+    x1 = Node(node.x0, node.y0, w_1, h_1) # top left
+    recursive_subdivide(x1, k, minPixelSize, img)
+
+    x2 = Node(node.x0, node.y0+h_1, w_1, h_2) # btm left
+    recursive_subdivide(x2, k, minPixelSize, img)
+
+    x3 = Node(node.x0 + w_1, node.y0, w_2, h_1)# top right
+    recursive_subdivide(x3, k, minPixelSize, img)
+
+    x4 = Node(node.x0+w_1, node.y0+h_1, w_2, h_2) # btm right
+    recursive_subdivide(x4, k, minPixelSize, img)
+
+    node.children = [x1, x2, x3, x4]
+   
+
+def find_children(node):
+   if not node.children:
+       return [node]
+   else:
+       children = []
+       for child in node.children:
+           children += (find_children(child))
+   return children
+```
+
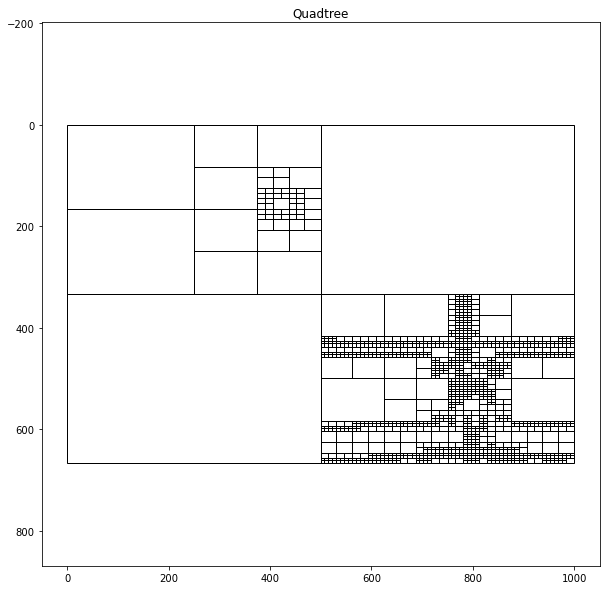
+If we partition the same image using two different sets of hyperparameters, we can see how we can manipulate how much the quadtree algorithm partitions the image.
+If we set the sum of square error threshold low, the quadtree will produce many cells, where if we assign the threshold high, it will create fewer cells.
+
+```python
+qtTemp = QTree(4, 3, img)  #contrast threshold, min cell size, img
+qtTemp.subdivide() # recursively generates quad tree
+qtTemp.graph_tree()
+
+qtTemp2 = QTree(9, 5, img) 
+qtTemp2.subdivide()
+qtTemp2.graph_tree()
+```
+
+![render of quadtree with small cells](media/quadtree/output_11_1.png)
+
+![render of quadtree with large cells](media/quadtree/output_11_3.png)
+
+As a final esthetic, I want to display the rendered version alongside the original photograph.
+For the sake of simplicity, I am adding a white border surrounding the two images and contacting them together to form a diptych.
+
+```python
+def concat_images(img1, img2, boarder=5, color=(255,255,255)):
+    img1_boarder = cv2.copyMakeBorder(
+                 img1, 
+                 boarder, #top
+                 boarder, #btn
+                 boarder, #left
+                 boarder, #right
+                 cv2.BORDER_CONSTANT, 
+                 value=color
+              )
+    img2_boarder = cv2.copyMakeBorder(
+                 img2, 
+                 boarder, #top
+                 boarder, #btn
+                 0, #left
+                 boarder, #right
+                 cv2.BORDER_CONSTANT, 
+                 value=color
+              )
+    return np.concatenate((img1_boarder, img2_boarder), axis=1)
+```
+
+Next, we wrap our quadtree algorithm with our output visualization to make creating the diptychs easier.
+The left is the original image, where the right is the rendered quadtree version.
+Each leaf node in the quadtree gets visualized by taking the average pixel values from the cell.
+Moreover, I added an outline to each cell to emphasize the cells produced.
+I found that either a red or black outline worked the best.
+
+```python
+def displayQuadTree(img_name, threshold=7, minCell=3, img_boarder=20, line_boarder=1, line_color=(0,0,255)):
+    imgT= cv2.imread(img_name)
+    qt = QTree(threshold, minCell, imgT) 
+    qt.subdivide()
+    qtImg= qt.render_img(thickness=line_boarder, color=line_color)
+    file_name = "output/" + img_name.split("/")[-1]
+    cv2.imwrite(file_name,qtImg)
+    file_name_2 = "output/diptych-" + img_name[-6] + img_name[-5] + ".jpg"
+    hConcat = concat_images(imgT, qtImg, boarder=img_boarder, color=(255,255,255))
+    cv2.imwrite(file_name_2,hConcat)
+    printI(hConcat)
+
+displayQuadTree("night2.jpg", threshold=3, img_boarder=20, line_color=(0,0,0), line_boarder = 1)
+```
+
+![street light diptych](media/quadtree/output_16_0.png)
+
+Every time I see these images, I  think about how humans, cameras, and algorithms view and interpret reality.
+
+```python
+displayQuadTree("night4.jpg", threshold=5)
+```
+
+![magic studio sign diptych](media/quadtree/output_18_0.png)
+
+In particular, night photography pairs remarkably well with this algorithm since many esthetics that night photographers have picked up distorts reality.
+Humans can rarely see vivid stars in the night nor light trails, yet if you set a camera with a long enough exposure, you will capture just that: and it is beautiful.
+With the increased prevalence of post-processing and filters on cameras, the photos we see now are never perfect representations of reality.
+
+```python
+displayQuadTree("../final/russell-final-1.jpg", threshold=12, line_color=(0,0,0))
+```
+
+![rit bus diptych](media/quadtree/output_20_0.png)
+
+I'm still vexed as to whether these distortions of reality are a good thing or a bad thing, or if this distinction is even pertinent.
+
+
+```python
+displayQuadTree("../final/russell-final-4.jpg", threshold=12, line_color=(0,0,0))
+```
+
+![diptych of street lights](media/quadtree/output_22_0.png)
+
+
+I am intrigued as to how detail are both illuminated and hidden away using the quadtrees.
+The main composition of the image remains unchanged, yet the more subtle details are cast away.
+
+
+```python
+displayQuadTree("../final/russell-final-7.jpg", threshold=12, line_color=(0,0,0))
+```
+
+![car headlight diptych](media/quadtree/output_24_0.png)
+
+
+```python
+displayQuadTree("../final/russell-final-10.jpg", threshold=12, line_color=(0,0,255))
+```
+
+![night shadows diptych](media/quadtree/output_25_0.png)
+
+
+```python
+displayQuadTree("../final/russell-final-14.jpg", threshold=12, line_color=(0,0,0))
+```
+
+![rit magic studio diptych](media/quadtree/output_26_0.png)
+
+Despite being intuitively aware of the differences between reality and the images we see, it is hard for our minds to quantify this stark difference.
+On the one hand, these images are the only thing that I have from my nights out at RIT doing photography, thus making these images evidence of my experience-- the only tangible thing I can cling onto. 
+Yet, on the other hand, it fails to capture the essence of RIT at night altogether. 
+I framed these images with a tripod, and their long exposure shots distort light in a way that the human eye can't perceive.
+The edits with both Lightroom and my python script further distorts the original scene.
+
+The problem with seeing the world through a camera is that you miss everything the camera doesn't see.
+I can't show you precisely what last night's sky looked like, not really, but you can see tonight's, and it will be beautiful.
+
+![](media/quadtree/full.jpg)