Fixed merge conflicts

5 years ago · 09be5d371b
--- a/blog/renderBlogPost.js
+++ b/blog/renderBlogPost.js
@ -4,7 +4,7 @@ const utils = require('../utils/utils.js');

 const sql = require('../utils/sql');

 const argsFull = '-S --base-header-level=1 --toc --toc-depth=3 -N --normalize -s --mathjax -t html5';
 const argsFull = '--from markdown-markdown_in_html_blocks+raw_html -S --base-header-level=1 --toc --toc-depth=3 -N --normalize -s --mathjax -t html5';
 const argsPreview = '-S --normalize -s --mathjax -t html5';


@ -127,6 +127,18 @@ module.exports=
                    }


                    var regExp = /\<customHTML .*?>/;
                    while (result.search(regExp) != -1)
                    {
                        const pathName =  "blogContent/posts/" + categoryURL + "/html/"
                            + postURL + ".html";

                        var htmlContent = utils.getFileContents(pathName).toString();

                        result = result.split("<customHTML />").join(htmlContent);
                    }


                    if(blocks == -1)
                        resolve(result);

--- a/blogContent/headerImages/gitHubGraphs.png
+++ b/blogContent/headerImages/gitHubGraphs.png
--- a/blogContent/posts/data-science/html/lets-build-a-genetic-algorithm.html
+++ b/blogContent/posts/data-science/html/lets-build-a-genetic-algorithm.html
@ -0,0 +1,484 @@
 <script type="text/javascript" src="https://www.gstatic.com/charts/loader.js"></script>
 <script
        src="https://code.jquery.com/jquery-3.3.1.slim.min.js"
        integrity="sha256-3edrmyuQ0w65f8gfBsqowzjJe2iM6n0nKciPUp8y+7E="
        crossorigin="anonymous">
 </script>
 <script>
    class Gene
    {
        /**
         * Constructs a new Gene to store in a chromosome.
         * @param min minimum value that this gene can store
         * @param max value this gene can possibly be
         * @param value normalized value
         */
        constructor(min, max, value)
        {
            this.min = min;
            this.max = max;
            this.value = value;
        }
        /**
         * De-normalizes the value of the gene
         * @returns {*}
         */
        getRealValue()
        {
            return (this.max - this.min) * this.value + this.min;
        }
        getValue()
        {
            return this.value;
        }
        setValue(val)
        {
            this.value = val;
        }
        makeClone()
        {
            return new Gene(this.min, this.max, this.value);
        }
        makeRandomGene()
        {
            return new Gene(this.min, this.max, Math.random());
        }
    }
    class Chromosome
    {
        /**
         * Constructs a chromosome by making a copy of
         * a list of genes.
         * @param geneArray
         */
        constructor(geneArray)
        {
            this.genes = [];
            for(let i = 0; i < geneArray.length; i++)
            {
                this.genes.push(geneArray[i].makeClone());
            }
        }
        getGenes()
        {
            return this.genes;
        }
        /**
         * Mutates a random gene.
         */
        mutate()
        {
            this.genes[Math.round(Math.random() * (this.genes.length-1))].setValue(Math.random());
        }
        /**
         * Creates a totally new chromosome with same
         * genetic structure as this chromosome but different
         * values.
         * @returns {Chromosome}
         */
        createRandomChromosome()
        {
            let geneAr = [];
            for(let i = 0; i < this.genes.length; i++)
            {
                geneAr.push(this.genes[i].makeRandomGene());
            }
            return new Chromosome(geneAr);
        }
    }
    /**
     * Mates two chromosomes using the blending method
     * and returns a list of 2 offspring.
     * @param father
     * @param mother
     * @returns {Chromosome[]}
     */
    const breed = function(father, mother)
    {
        let son = new Chromosome(father.getGenes());
        let daughter = new Chromosome(mother.getGenes());
        for(let i = 0;i < son.getGenes().length; i++)
        {
            let blendCoef = Math.random();
            blendGene(son.getGenes()[i], daughter.getGenes()[i], blendCoef);
        }
        return [son, daughter];
    };
    /**
     * Blends two genes together based on a random blend
     * coefficient.
     **/
    const blendGene = function(gene1, gene2, blendCoef)
    {
        let value1 = (blendCoef * gene1.getValue()) +
            (gene2.getValue() * (1- blendCoef));
        let value2 = ((1-blendCoef) * gene1.getValue()) +
            (gene2.getValue() * blendCoef);
        gene1.setValue(value1);
        gene2.setValue(value2);
    };
    /**
     * Helper function to sort an array
     *
     * @param prop name of JSON property to sort by
     * @returns {function(*, *): number}
     */
    function predicateBy(prop)
    {
        return function(a,b)
        {
            var result;
            if(a[prop] > b[prop])
            {
                result =  1;
            }
            else if(a[prop] < b[prop])
            {
                result = -1;
            }
            return result;
        }
    }
    /**
     * Function which computes the fitness of everyone in the
     * population and returns the most fit survivors. Method
     * known as elitism.
     *
     * @param population
     * @param keepNumber
     * @param fitnessFunction
     * @returns {{average: number,
     * survivors: Array, bestFit: Chromosome }}
     */
    const naturalSelection = function(population, keepNumber, fitnessFunction)
    {
        let fitnessArray = [];
        let total = 0;
        for(let i = 0; i < population.length; i++)
        {
            const fitness = fitnessFunction(population[i]);
            fitnessArray.push({fit:fitness, chrom: population[i]});
            total+= fitness;
        }
        fitnessArray.sort(predicateBy("fit"));
        let survivors = [];
        let bestFitness = fitnessArray[0].fit;
        let bestChromosome = fitnessArray[0].chrom;
        for(let i = 0; i < keepNumber; i++)
        {
            survivors.push(fitnessArray[i].chrom);
        }
        return {average: total/population.length, survivors: survivors, bestFit: bestFitness, bestChrom: bestChromosome};
    };
    /**
     * Randomly  everyone in the population
     *
     * @param population
     * @param desiredPopulationSize
     */
    const matePopulation = function(population, desiredPopulationSize)
    {
        const originalLength = population.length;
        while(population.length < desiredPopulationSize)
        {
            let index1 = Math.round(Math.random() * (originalLength-1));
            let index2 = Math.round(Math.random() * (originalLength-1));
            if(index1 !== index2)
            {
                const babies = breed(population[index1], population[index2]);
                population.push(babies[0]);
                population.push(babies[1]);
            }
        }
    };
    /**
     * Randomly mutates the population
     **/
    const mutatePopulation = function(population, mutatePercentage)
    {
        if(population.length >= 2)
        {
            let mutations = mutatePercentage *
                population.length *
                population[0].getGenes().length;
            for(let i = 0; i < mutations; i++)
            {
                population[i].mutate();
            }
        }
        else
        {
            console.log("Error, population too small to mutate");
        }
    };
    /**
     * Introduces x random chromosomes to the population.
     * @param population
     * @param immigrationSize
     */
    const newBlood = function(population, immigrationSize)
    {
        for(let i = 0; i < immigrationSize; i++)
        {
            let geneticChromosome = population[0];
            population.push(geneticChromosome.createRandomChromosome());
        }
    };
    let costx = Math.random() * 10;
    let costy = Math.random() * 10;
    /** Defines the cost as the "distance" to a 2-d point.
     * @param chromosome
     * @returns {number}
     */
    const basicCostFunction = function(chromosome)
    {
        return Math.abs(chromosome.getGenes()[0].getRealValue() - costx) +
            Math.abs(chromosome.getGenes()[1].getRealValue() - costy);
    };
    /**
     * Creates a totally random population based  on a desired size
     * and a prototypical chromosome.
     *
     * @param geneticChromosome
     * @param populationSize
     * @returns {Array}
     */
    const createRandomPopulation = function(geneticChromosome, populationSize)
    {
        let population = [];
        for(let i = 0; i < populationSize; i++)
        {
            population.push(geneticChromosome.createRandomChromosome());
        }
        return population;
    };
    /**
     * Runs the genetic algorithm by going through the processes of
     * natural selection, mutation, mating, and immigrations. This
     * process will continue until an adequately performing chromosome
     * is found or a generation threshold is passed.
     *
     * @param geneticChromosome Prototypical chromosome: used so algo knows
     *                            what the dna of the population looks like.
     * @param costFunction Function which defines how bad a Chromosome is
     * @param populationSize Desired population size for population
     * @param maxGenerations Cut off level for number of generations to run
     * @param desiredCost Sufficient cost to terminate program at
     * @param mutationRate Number between [0,1] representing proportion of genes
     * to mutate each generation
     * @param keepNumber Number of Organisms which survive each generation
     * @param newBloodNumber Number of random immigrants to introduce into
     * the population each generation.
     * @returns {*}
     */
    const runGeneticOptimization = function(geneticChromosome, costFunction,
                                            populationSize, maxGenerations,
                                            desiredCost, mutationRate, keepNumber,
                                            newBloodNumber)
    {
        let population = createRandomPopulation(geneticChromosome, populationSize);
        let generation = 0;
        let bestCost = Number.MAX_VALUE;
        let bestChromosome = geneticChromosome;
        do
        {
            matePopulation(population, populationSize);
            newBlood(population, newBloodNumber);
            mutatePopulation(population, mutationRate);
            let generationResult = naturalSelection(population, keepNumber, costFunction);
            if(bestCost > generationResult.bestFit)
            {
                bestChromosome = generationResult.bestChrom;
                bestCost = generationResult.bestFit;
            }
            population = generationResult.survivors;
            generation++;
            console.log("Generation " + generation + " Best Cost: " + bestCost);
        }while(generation < maxGenerations && bestCost > desiredCost);
        return bestChromosome;
    };
    /**
     * Ugly globals used to keep track of population state for the graph.
     */
    let genericChromosomeG, costFunctionG,
        populationSizeG, maxGenerationsG,
        desiredCostG, mutationRateG, keepNumberG,
        newBloodNumberG, populationG, generationG,
        bestCostG = Number.MAX_VALUE, bestChromosomeG = genericChromosomeG;
    const runGeneticOptimizationForGraph = function()
    {
        let generationResult = naturalSelection(populationG, keepNumberG, costFunctionG);
        stats.push([generationG, generationResult.bestFit, generationResult.average]);
        if(bestCostG > generationResult.bestFit)
        {
            bestChromosomeG = generationResult.bestChrom;
            bestCostG = generationResult.bestFit;
        }
        populationG = generationResult.survivors;
        generationG++;
        console.log("Generation " + generationG + " Best Cost: " + bestCostG);
        console.log(generationResult);
        matePopulation(populationG, populationSizeG);
        newBlood(populationG, newBloodNumberG);
        mutatePopulation(populationG, mutationRateG);
        createGraph();
    };
    let stats = [];
    const createGraph = function()
    {
        var dataPoints = [];
        console.log(dataPoints);
        var data = new google.visualization.DataTable();
        data.addColumn('number', 'Gene 1');
        data.addColumn('number', 'Gene 2');
        for(let i = 0; i < populationG.length; i++)
        {
            data.addRow([populationG[i].getGenes()[0].getRealValue(),
                populationG[i].getGenes()[1].getRealValue()]);
        }
        var options = {
            title: 'Genetic Evolution On Two Genes Generation: ' + generationG,
            hAxis: {title: 'Gene 1', minValue: 0, maxValue: 10},
            vAxis: {title: 'Gene 2', minValue: 0, maxValue: 10},
        };
        var chart = new google.visualization.ScatterChart(document.getElementById('chart_div'));
        chart.draw(data, options);
        //line chart stuff
        var line_data = new google.visualization.DataTable();
        line_data.addColumn('number', 'Generation');
        line_data.addColumn('number', 'Best');
        line_data.addColumn('number', 'Average');
        line_data.addRows(stats);
        console.log(stats);
        var lineChartOptions = {
            hAxis: {
                title: 'Generation'
            },
            vAxis: {
                title: 'Cost'
            },
            colors: ['#AB0D06', '#007329']
        };
        var chart = new google.visualization.LineChart(document.getElementById('line_chart'));
        chart.draw(line_data, lineChartOptions);
    };
    let gene1 = new Gene(1,10,10);
    let gene2 = new Gene(1,10,0.4);
    let geneList = [gene1, gene2];
    let exampleOrganism = new Chromosome(geneList);
    genericChromosomeG = exampleOrganism;
    costFunctionG = basicCostFunction;
    populationSizeG = 100;
    maxGenerationsG = 30;
    desiredCostG = 0.00001;
    mutationRateG = 0.3;
    keepNumberG = 30;
    newBloodNumberG = 10;
    generationG = 0;
    function verifyForm()
    {
        if(Number($("#populationSize").val()) <= 1)
        {
            alert("Population size must be greater than one.");
            return false;
        }
        if(Number($("#mutationRate").val()) > 1 ||
            Number($("#mutationRate").val()) < 0)
        {
            alert("Mutation rate must be between zero and one.");
            return false;
        }
        if(Number($("#survivalSize").val()) < 0)
        {
            alert("Survival size can't be less than one.");
            return false;
        }
        if(Number($("#newBlood").val()) < 0)
        {
            alert("New organisms can't be a negative number.");
            return false;
        }
        return true;
    }
    function resetPopulation()
    {
        if(verifyForm())
        {
            stats = [];
            autoRunning = false;
            $("#runAutoOptimizer").val("Auto Run");
            populationSizeG = $("#populationSize").val();
            mutationRateG = $("#mutationRate").val();
            keepNumberG = $("#survivalSize").val();
            newBloodNumberG = $("#newBlood").val();
            generationG = 0;
            populationG = createRandomPopulation(genericChromosomeG, populationSizeG);
            createGraph();
        }
    }
    populationG = createRandomPopulation(genericChromosomeG, populationSizeG);
    window.onload = function (){
        google.charts.load('current', {packages: ['corechart', 'line']});
        google.charts.load('current', {'packages':['corechart']}).then(function()
        {
            createGraph();
        })
    };
    let autoRunning = false;
    function runAutoOptimizer()
    {
        if(autoRunning === true)
        {
            runGeneticOptimizationForGraph();
            setTimeout(runAutoOptimizer, 1000);
        }
    }
    function startStopAutoRun()
    {
        autoRunning = !autoRunning;
        if(autoRunning)
        {
            $("#runAutoOptimizer").val("Stop Auto Run");
        }
        else
        {
            $("#runAutoOptimizer").val("Resume Auto Run");
        }
        runAutoOptimizer();
    }
 </script>
 <div id="chart_div"></div>
 <div id="line_chart"></div>
 <input class='btn btn-primary' id="runOptimizer" onclick='runGeneticOptimizationForGraph()' type="button" value="Next Generation">
 <input class='btn btn-primary' id="runAutoOptimizer" onclick='startStopAutoRun()' type="button" value="Auto Run">
 <br>
 <br>
 <div class="card">
    <div class="card-header">
        <h2>Population Variables</h2>
    </div>
    <form class="card-body">
        <div class="row p-2">
            <div class="col">
                <label for="populationSize">Population Size</label>
                <input type="text" class="form-control" value="100" id="populationSize" placeholder="Population Size" required>
            </div>
            <div class="col">
                <label for="populationSize">Survival Size</label>
                <input type="text" class="form-control" value="20" id="survivalSize" placeholder="Survival Size" required>
            </div>
        </div>
        <div class="row p-2">
            <div class="col">
                <label for="populationSize">Mutation Rate</label>
                <input type="text" class="form-control" value="0.03" id="mutationRate" placeholder="Mutation Rate" required>
            </div>
            <div class="col">
                <label for="populationSize">New Organisms Per Generation</label>
                <input type="text" class="form-control" value="5" id="newBlood" placeholder="New Organisms" required>
            </div>
        </div>
        <br>
        <input class='btn btn-primary' id="reset" onclick='resetPopulation()' type="button" value="Reset Population">
    </form>
 </div>
--- a/blogContent/posts/data-science/lets-build-a-genetic-algorithm.md
+++ b/blogContent/posts/data-science/lets-build-a-genetic-algorithm.md
@ -0,0 +1,515 @@
 # Live Simulation

 <customHTML />

 # Background and Theory

 Since you stumbled upon this article, you might be wondering what the heck genetic algorithms are.
 To put it simply: genetic algorithms employ the same tactics used in natural selection to find an optimal solution to an optimization problem.
 Genetic algorithms are often used in high dimensional problems where the optimal solutions are not apparent.
 Genetic algorithms are commonly used to tune the [hyper-parameters](https://en.wikipedia.org/wiki/Hyperparameter) of a program.
 However, this algorithm can be used in any scenario where you have a function which defines how well a solution is.
 Many people have used genetic algorithms in video games to auto learn the weaknesses of players.

 The beautiful part about Genetic Algorithms are their simplicity; you need absolutely no knowledge of linear algebra or calculus.
 To implement a genetic algorithm from scratch you only need **very basic** algebra and a general grasp of evolution.

 # Genetic Algorithm

 All genetic algorithms typically have a single cycle where you continuously mutate, breed, and select the most optimal solutions.
 I will dive into each section of this algorithm using simple JavaScript code snippets.
 The algorithm which I present is very generic and modular so it should be easy to port into other programming languages and applications. 

 ![Genetic Algorithms Flow Chart](media/GA/GAFlowChart.svg)


 ## Population Creation

 The very first thing we need to do is specify a data-structure for storing our genetic information.
 In biology, chromosomes are composed of sequences of genes.
 Many people run genetic algorithms on binary arrays since they more closely represent DNA.
 However, as computer scientists, it is often easier to model problems using continuous numbers.
 In this approach, every gene will be a single floating point number ranging between zero and one.
 Every type of gene will have a max and min value which represents the absolute extremes of that gene.
 This works well for optimization because it allows us to easily limit our search space. 
 For example, we can specify that "height" gene can only vary between 0 and 90.
 To get the actual value of the gene from its \[0-1] value we simple de-normalize it.

 $$
 g_{real value} = (g_{high}- g_{low})g_{norm} + g_{low}
 $$

 ```javascript
 class Gene
 {
    /**
     * Constructs a new Gene to store in a chromosome.
     * @param min minimum value that this gene can store
     * @param max value this gene can possibly be
     * @param value normalized value
     */
    constructor(min, max, value)
    {
        this.min = min;
        this.max = max;
        this.value = value;
    }

    /**
     * De-normalizes the value of the gene
     * @returns {*}
     */
    getRealValue()
    {
        return (this.max - this.min) * this.value + this.min;
    }

    getValue()
    {
        return this.value;
    }

    setValue(val)
    {
        this.value = val;
    }

    makeClone()
    {
        return new Gene(this.min, this.max, this.value);
    }

    makeRandomGene()
    {
        return new Gene(this.min, this.max, Math.random());
    }
 }
 ```


 Now that we have genes, we can create chromosomes. 
 Chromosomes are simply collections of genes.
 Whatever language you make this in, make sure that when you create a new chromosome it 
 is has a [deep copy](https://en.wikipedia.org/wiki/Object_copying) of the original genetic information rather than a shallow copy.
 A shallow copy is when you simple copy the object pointer where a deep copy is actually creating a new object.
 If you fail to do a deep copy, you will have weird issues where multiple chromosomes will share the same DNA.

 In this class I added helper functions to clone the chromosome as a random copy. 
 You can only create a new chromosome by cloning because I wanted to keep the program generic and make no assumptions about the domain.
 Since you only provide the min/max information for the genes once, cloning an existing chromosome is the easiest way of
 ensuring that all corresponding chromosomes contain genes with identical extrema. 


 ```javascript
 class Chromosome
 {
    /**
     * Constructs a chromosome by making a copy of
     * a list of genes.
     * @param geneArray
     */
    constructor(geneArray)
    {
        this.genes = [];
        for(let i = 0; i < geneArray.length; i++)
        {
            this.genes.push(geneArray[i].makeClone());
        }
    }

    getGenes()
    {
        return this.genes;
    }

    /**
     * Mutates a random gene.
     */
    mutate()
    {
        this.genes[Math.round(Math.random() * (this.genes.length-1))].setValue(Math.random());
    }

    /**
     * Creates a totally new chromosome with same
     * genetic structure as this chromosome but different
     * values.
     * @returns {Chromosome}
     */
    createRandomChromosome()
    {
        let geneAr = [];
        for(let i = 0; i < this.genes.length; i++)
        {
            geneAr.push(this.genes[i].makeRandomGene());
        }
        return new Chromosome(geneAr);
    }
 }
 ```

 Creating a random population is pretty straight forward if implemented a method to create a random clone of a chromosome. 

 ```javascript
 /**
 * Creates a totally random population based  on a desired size
 * and a prototypical chromosome.
 *
 * @param geneticChromosome
 * @param populationSize
 * @returns {Array}
 */
 const createRandomPopulation = function(geneticChromosome, populationSize)
 {
    let population = [];
    for(let i = 0; i < populationSize; i++)
    {
        population.push(geneticChromosome.createRandomChromosome());
    }
    return population;
 };
 ```

 This is where nearly all the domain information is introduced. 
 After you define what types of genes are found on each chromosome, you can create an entire population.
 In this example all genes contain values ranging between one and ten. 

 ```javascript
 let gene1 = new Gene(1,10,10);
 let gene2 = new Gene(1,10,0.4);
 let geneList = [gene1, gene2];

 let exampleOrganism = new Chromosome(geneList);

 let population = createRandomPopulation(genericChromosome, 100);
 ```


 ## Evaluate Fitness

 Like all optimization problems, you need a way to evaluate the performance of a particular solution.
 The cost function takes in a chromosome and evaluates how close it got to the ideal solution. 
 This particular example it is just computing the [Manhattan Distance](https://en.wiktionary.org/wiki/Manhattan_distance) to a random 2D point.
 I chose two dimensions because it is easy to graph, however, real applications may have dozens of genes on each chromosome. 

 ```javascript
 let costx = Math.random() * 10;
 let costy = Math.random() * 10;

 /** Defines the cost as the "distance" to a 2-d point.
 * @param chromosome
 * @returns {number}
 */
 const basicCostFunction = function(chromosome)
 {
    return Math.abs(chromosome.getGenes()[0].getRealValue() - costx) +
        Math.abs(chromosome.getGenes()[1].getRealValue() - costy);
 };
 ```

 ## Selection

 Selecting the best performing chromosomes is straightforward after you have a function for evaluating the performance.
 This code snippet also computes the average and best chromosome of the population to make it easier to graph and define
 the stopping point for the algorithm's main loop. 

 ```javascript
 /**
 * Function which computes the fitness of everyone in the
 * population and returns the most fit survivors. Method
 * known as elitism.
 *
 * @param population
 * @param keepNumber
 * @param fitnessFunction
 * @returns {{average: number,
 * survivors: Array, bestFit: Chromosome }}
 */
 const naturalSelection = function(population, keepNumber, fitnessFunction)
 {
    let fitnessArray = [];
    let total = 0;
    for(let i = 0; i < population.length; i++)
    {
        const fitness = fitnessFunction(population[i]);
        fitnessArray.push({fit:fitness, chrom: population[i]});
        total+= fitness;
    }

    fitnessArray.sort(predicateBy("fit"));

    let survivors = [];
    let bestFitness = fitnessArray[0].fit;
    let bestChromosome = fitnessArray[0].chrom;
    for(let i = 0; i < keepNumber; i++)
    {
        survivors.push(fitnessArray[i].chrom);
    }
    return {average: total/population.length, survivors: survivors, bestFit: bestFitness, bestChrom: bestChromosome};
 };
 ```

 You might be wondering how I sorted the list of JSON objects - not a numerical array.
 I used the following function as a comparator for JavaScript's built in sort function.
 This comparator will compare objects based on a specific attribute that you give it.
 This is a very handy function to include in all of your JavaScript projects for easy sorting. 

 ```javascript
 /**
 * Helper function to sort an array
 *
 * @param prop name of JSON property to sort by
 * @returns {function(*, *): number}
 */
 function predicateBy(prop)
 {
    return function(a,b)
    {
        var result;
        if(a[prop] > b[prop])
        {
            result =  1;
        }
        else if(a[prop] < b[prop])
        {
            result = -1;
        }
        return result;
    }
 }
 ```

 ## Reproduction

 The process of reproduction can be broken down into Pairing and Mating. 

 ### Pairing

 Pairing is the process of selecting mates to produce offspring.
 A typical approach will separate the population into two segments of mothers and fathers.
 You then randomly pick pairs of mothers and fathers to produce offspring.
 It is ok if one chromosome mates more than once.
 It is just important that you keep this process random. 

 ```javascript
 /**
 * Randomly  everyone in the population
 *
 * @param population
 * @param desiredPopulationSize
 */
 const matePopulation = function(population, desiredPopulationSize)
 {
    const originalLength = population.length;
    while(population.length < desiredPopulationSize)
    {
        let index1 = Math.round(Math.random() * (originalLength-1));
        let index2 = Math.round(Math.random() * (originalLength-1));
        if(index1 !== index2)
        {
            const babies = breed(population[index1], population[index2]);
            population.push(babies[0]);
            population.push(babies[1]);
        }
    }
 };
 ```

 ### Mating

 Mating is the actual act of forming new chromosomes/organisms based on your previously selected pairs.
 From my research, there are two major forms of mating: blending, crossover.

 Blending is typically the most preferred approach to mating when dealing with continuous variables.
 In this approach you combine the genes of both parents based on a random factor.

 $$
 c_{new} = r * c_{mother} + (1-r) * c_{father}
 $$

 The second offspring simply uses (1-r) for their random factor to adjust the chromosomes. 

 Crossover is the simplest approach to mating.
 In this process you clone the parents and then you randomly swap *n* of their genes.
 This works fine in some scenarios; however, this severely lacks the genetic diversity of the genes because you now have to solely
 rely on mutations for changes. 

 ```javascript
 /**
 * Mates two chromosomes using the blending method
 * and returns a list of 2 offspring.
 * @param father
 * @param mother
 * @returns {Chromosome[]}
 */
 const breed = function(father, mother)
 {
    let son = new Chromosome(father.getGenes());
    let daughter = new Chromosome(mother.getGenes());

    for(let i = 0;i < son.getGenes().length; i++)
    {
        let blendCoef = Math.random();
        blendGene(son.getGenes()[i], daughter.getGenes()[i], blendCoef);
    }
    return [son, daughter];
 };

 /**
 * Blends two genes together based on a random blend
 * coefficient.
 **/
 const blendGene = function(gene1, gene2, blendCoef)
 {
    let value1 = (blendCoef * gene1.getValue()) +
        (gene2.getValue() * (1- blendCoef));
    let value2 = ((1-blendCoef) * gene1.getValue()) +
        (gene2.getValue() * blendCoef);

    gene1.setValue(value1);
    gene2.setValue(value2);
 };
 ```

 ## Mutation

 Mutations are random changes to an organisms DNA.
 In the scope of genetic algorithms, it helps our population converge on the correct solution.

 You can either adjust genes by a factor resulting in a smaller change or, you can
 change the value of the gene to be something completely random.
 Since we are using the blending technique for reproduction, we already have small incremental changes.
 I prefer to use mutations to randomly change the entire gene since it helps prevent the algorithm 
 from settling on a local minimum rather than the global minimum. 


 ```javascript
 /**
 * Randomly mutates the population
 **/
 const mutatePopulation = function(population, mutatePercentage)
 {
    if(population.length >= 2)
    {
        let mutations = mutatePercentage *
                        population.length *
                        population[0].getGenes().length;
        for(let i = 0; i < mutations; i++)
        {
            population[i].mutate();
        }
    }
    else
    {
        console.log("Error, population too small to mutate");
    }
 };
 ```

 ## Immigration

 Immigration or "new blood" is the process of dumping random organisms into your population at each generation.
 This prevents us from getting stuck in a local minimum rather than the global minimum.
 There are more advanced techniques to accomplish this same concept.
 My favorite approach (not implemented here) is raising **x** populations simultaneously and every **y** generations
 you take **z** organisms from each population and move them to another population. 

 ```javascript
 /**
 * Introduces x random chromosomes to the population.
 * @param population
 * @param immigrationSize
 */
 const newBlood = function(population, immigrationSize)
 {
    for(let i = 0; i < immigrationSize; i++)
    {
        let geneticChromosome = population[0];
        population.push(geneticChromosome.createRandomChromosome());
    }
 };
 ```

 ## Putting It All Together

 Now that we have all the ingredients for a genetic algorithm we can piece it together in a simple loop.

 ```javascript
 /**
 * Runs the genetic algorithm by going through the processes of
 * natural selection, mutation, mating, and immigrations. This
 * process will continue until an adequately performing chromosome
 * is found or a generation threshold is passed.
 *
 * @param geneticChromosome Prototypical chromosome: used so algo knows
 *                            what the dna of the population looks like.
 * @param costFunction Function which defines how bad a Chromosome is
 * @param populationSize Desired population size for population
 * @param maxGenerations Cut off level for number of generations to run
 * @param desiredCost Sufficient cost to terminate program at
 * @param mutationRate Number between [0,1] representing proportion of genes
 * to mutate each generation
 * @param keepNumber Number of Organisms which survive each generation
 * @param newBloodNumber Number of random immigrants to introduce into
 * the population each generation.
 * @returns {*}
 */
 const runGeneticOptimization = function(geneticChromosome, costFunction,
                                        populationSize, maxGenerations,
                                        desiredCost, mutationRate, keepNumber,
                                        newBloodNumber)
 {
    let population = createRandomPopulation(geneticChromosome, populationSize);
    let generation = 0;
    let bestCost = Number.MAX_VALUE;
    let bestChromosome = geneticChromosome;
    do
    {
        matePopulation(population, populationSize);
        newBlood(population, newBloodNumber);
        mutatePopulation(population, mutationRate);
        let generationResult = naturalSelection(population, keepNumber, costFunction);

        if(bestCost > generationResult.bestFit)
        {
            bestChromosome = generationResult.bestChrom;
            bestCost = generationResult.bestFit;
        }
        population = generationResult.survivors;

        generation++;
        console.log("Generation " + generation + " Best Cost: " + bestCost);
    }while(generation < maxGenerations && bestCost > desiredCost);
    return bestChromosome;
 };
 ```


 ## Running

 Running the program is pretty straight forward after you have your genes and cost function defined.
 You might be wondering if there is an optimal configuration of parameters to use with this algorithm.
 The answer is that it varies based on the particular problem.
 Problems like the one graphed by this website perform very well with a low mutation rate and a high population.
 However, some higher dimensional problems won't even converge on a local answer if you set your mutation rate too low. 

 ```javascript
 let gene1 = new Gene(1,10,10);
 ...
 let geneN = new Gene(1,10,0.4);
 let geneList = [gene1,..., geneN];

 let exampleOrganism = new Chromosome(geneList);

 costFunction = function(chromosome)
 {
    var d =...;
    //compute cost
    return d;
 }

 runGeneticOptimization(exampleOrganism, costFunction, 100, 50, 0.01, 0.3, 20, 10);
 ```

 The complete code for the genetic algorithm and the fancy JavaScript graphs can be found in my [Random Scripts GitHub Repository](https://github.com/jrtechs/RandomScripts).
 In the future I may package this into an [npm](https://www.npmjs.com/) package.
--- a/blogContent/posts/data-science/media/GA/GAFlowChart.svg
+++ b/blogContent/posts/data-science/media/GA/GAFlowChart.svg
--- a/blogContent/posts/projects/github-graphs-project.md
+++ b/blogContent/posts/projects/github-graphs-project.md
@ -0,0 +1,72 @@
 Shortly after working on my [Steam Friends Graph](https://jrtechs.net/projects/steam-friends-graph)
 ,I had the idea of extending the project to include the GitHub network.
 I used [BrickHack V](https://brickhack.io/) as the opportunity to work on this project with my friends.
 Rather than simply use the code that was used in the Steam friends graph, the architecture was completely
 revamped to reflect both the differences between the Steam and GitHub networks and my improved web development skills.

 # Project Overview

 We created an interactive website which allows you to make graphs based on the Github network. 
 Currently the site generates three types of graphs-- the most popular and entertaining of which is the friends graph. 
 The friends graph helps you visualize clusters of friends/collaborators on GitHub.
 Similar to the Steam Friends Project, I hope that this project will make people more interested in learning about big data.
 The visual aspect of this website makes learning about topics such as clustering and graph databases more intuitive.


 ## Friends View

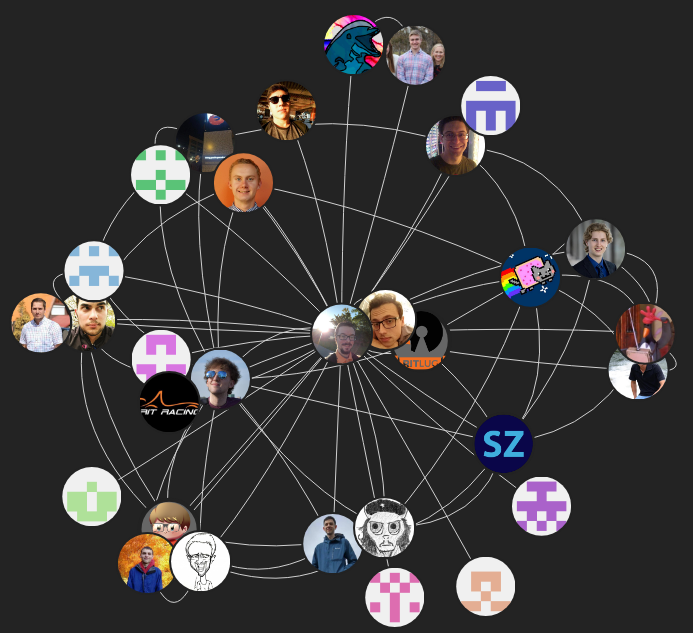
 ![Friends Graph of JrTechs](media/github/jrtechsGraph.png)

 The friends view displays all of the people which you following and your followers.
 This also connects connects everyone in the graph which are following each other.

 ## Repository View

 ![Repositories Timeline for JrTechs](media/github/RepositoriesView.png)

 ## Organization View

 ![Organization view for RITlug](media/github/ritlugOrg.png)

 ![Organization view for FOSS@MAGIC](media/github/fossRITOrg.png)


 ## Technologies Used

 - [BootStrap](https://getbootstrap.com/)
 - [jQuery](https://jquery.com/)
 - [Vis JS](http://visjs.org/)
 - [Github v3 API](https://developer.github.com/v3/) 
 - [Node.js](https://nodejs.org/en/) 

 # Changes From the Steam Graph Project

 The one stark difference between the Steam network and GitHub is the amount of friends that people have.
 Most developers on GitHub typically only follows around 20 people where it is not uncommon for people on Steam to have well over 100 friends.
 Due to the smaller graphs, I was able to use VisJS which has nicer animations and supports custom HTML for each node.

 ![Jrtechs Steam Friends Network](media/steam/jrtechs1.png)

 Another big change to the architecture was the way in which graphs are sent to the client.
 The server generated the graph and then sent the nodes and edges to the client over a web socket for the steam graph.
 In this project, the client builds the graph and queries the server using ajax for the necessary information.
 This gives the client a more dynamic loading progress and makes hosting the application much easier. 

 # Future Work

 Since this project was initially created during a hackathon, there is a **lot** of work to be done.
 I will outline a few ideas which I have.

 - Improved Caching and Performance
 - Friends of Friends -- similar to Steam's graph
 - Graphs Linking Users and Repositories Based on Activity
 - Code Metrics

 # Contributing

 If you want to contribute to this project and don't know where to start, look at the open issues on [GitHub](https://github.com/jrtechs/github-graphs).
 Once you know what you want to work on, just discuss it in the issues and file a pull request.
 I are very open to new contributes.


 <youtube src="rz7KD_d-uQg" />
--- a/blogContent/posts/projects/media/github/RepositoriesView.png
+++ b/blogContent/posts/projects/media/github/RepositoriesView.png
--- a/blogContent/posts/projects/media/github/fossRITOrg.png
+++ b/blogContent/posts/projects/media/github/fossRITOrg.png
--- a/blogContent/posts/projects/media/github/jrtechsGraph.png
+++ b/blogContent/posts/projects/media/github/jrtechsGraph.png
--- a/blogContent/posts/projects/media/github/ritlugOrg.png
+++ b/blogContent/posts/projects/media/github/ritlugOrg.png
--- a/templates/blog/blogMain.html
+++ b/templates/blog/blogMain.html
@ -32,19 +32,14 @@
                <br><br>
            {/for}


            {>paginationTemplate}
            <br>
        </div>
        <div class="col-md-4 col-4">
        <div class="col-md-4 col-12">
            {>sideBar}
        </div>
    </div>



 </div>



 {footer}
--- a/templates/blog/paginationBar.html
+++ b/templates/blog/paginationBar.html
@ -1,6 +1,6 @@
 {if pagination}
 <div class="row justify-content-center w-100">
    <div class="col-6">
    <div class="col-md-6 col-12">
        <nav aria-label="...">
            <ul class="pagination">
                {if pagination.previous}
--- a/templates/blog/sideBar.html
+++ b/templates/blog/sideBar.html
@ -4,6 +4,8 @@
            <h5 class="mb-1">Project Sites</h5>
        </a>
        <a class="list-group-item" href='https://jrtechs.net/steam/'>Steam Graph Analysis<br></a>
        <a class="list-group-item" href='https://video.jrtechs.net'>Home Brew Plex Server<br></a>
        <a class="list-group-item" href='https://github-graphs.com/'>GitHub Graphs<br></a>
        <a class="list-group-item" href='https://jrtechs.me/'>Portfolio<br></a>
        <a class="list-group-item" href='https://clubpanda.jrtechs.net/'>Club Panda<br></a>
    </div>